题目内容
8. OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )| A. | 80° | B. | 40° | C. | 50° | D. | 20° |
分析 直接根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,求解即可求得答案.
解答 解:∵∠C=40°,
∴∠AOB=2∠C=80°.
故选A.
点评 此题考查了圆周角定理.注意熟记定理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.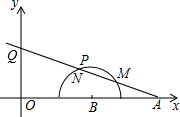 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | $\frac{8}{15}$$\sqrt{3}$ | C. | 2-$\frac{4}{5}$$\sqrt{3}$ | D. | 2$\sqrt{3}$-2 |
13.下列变形正确的是( )
| A. | $\frac{m}{n}=\frac{{m}^{2}}{{n}^{2}}$ | B. | $\frac{2}{5+y}=\frac{2x}{5x+y}$ | ||
| C. | $\frac{-x}{x-y}=\frac{x}{-x+y}$ | D. | $\frac{x+0.23y}{0.5x-y}=\frac{x-23y}{50x-y}$ |
17.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{{x}^{2}+1}{2}$,$\frac{3xy}{7}$,$\frac{3}{x+y}$,x+$\frac{1}{y}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18. 如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )
如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )
 如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )
如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )| A. | 18 | B. | 15 | C. | 13 | D. | 12 |
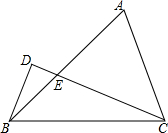 如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.
如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.