题目内容
13.下列变形正确的是( )| A. | $\frac{m}{n}=\frac{{m}^{2}}{{n}^{2}}$ | B. | $\frac{2}{5+y}=\frac{2x}{5x+y}$ | ||
| C. | $\frac{-x}{x-y}=\frac{x}{-x+y}$ | D. | $\frac{x+0.23y}{0.5x-y}=\frac{x-23y}{50x-y}$ |
分析 利用分式的基本性质,逐项分析即可.
解答 A.$\frac{m}{n}$=$\frac{{m}^{2}}{nm}$(m≠0)或$\frac{m}{n}=\frac{mn}{{n}^{2}}$,所以此选项错误;
B.$\frac{2}{5+y}=\frac{2x}{5x+xy}$,所以此选项错误;
C.$\frac{-x}{x-y}=\frac{x}{-x+y}$,所以此选项正确;
D.$\frac{x+0.23y}{0.5x-y}=\frac{x-23y}{50x-100y}$,所以此选项错误,
故选C.
点评 此题主要考查了分式的基本性质,利用分式的基本性质:(1)分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.(2)分式中的符号法则:分子、分母、分式本身同时改变两处的符号,分式的值不变,是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.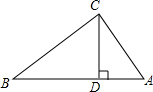 如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
 如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )| A. | 1.6 | B. | 2.4 | C. | 2 | D. | 2.1 |
8. OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
 OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )| A. | 80° | B. | 40° | C. | 50° | D. | 20° |
5.下列方程中,是一元一次方程的是( )
| A. | x+4y=1 | B. | x2-2x=3 | C. | 2x-$\frac{x}{3}$=1-$\frac{3x}{2}$ | D. | xy+6=3z |
 如图,?ABCD的对角线AC、BD交于点O,E、G在直线AC上,AE=CG,F、H直线BD上,BF=DH,求证:EF=HG.
如图,?ABCD的对角线AC、BD交于点O,E、G在直线AC上,AE=CG,F、H直线BD上,BF=DH,求证:EF=HG.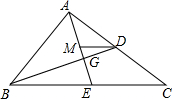 如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.
如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.