题目内容
18.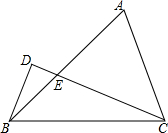 如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.
如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.
分析 延长BD至F,使得DF=BD,连结CF交AB于G.根据中垂线的性质和等腰直角三角形的判定和性质得到CF=2$\sqrt{2}$,BG=CG=2,根据线段的和差求得FG=2$\sqrt{2}$-2,
在Rt△BGF中,根据勾股定理即可求解.
解答 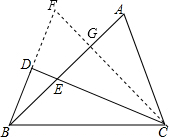 解:延长BD至F,使得DF=BD,连结CF交AB于G.
解:延长BD至F,使得DF=BD,连结CF交AB于G.
∵BD⊥CD,DF=BD,
∴CF=CB=2$\sqrt{2}$,∠DCF=∠ECB,
∵∠ABC=45°=2∠ECB,
∴∠BCG=45°,
∴△BCG是等腰直角三角形,
∵BC=2$\sqrt{2}$,
∴BG=CG=$\frac{\sqrt{2}}{2}$BC=2,
∴FG=2$\sqrt{2}$-2,
在Rt△BGF中,(2BD)2=BF2=BG2+FG2=22+(2$\sqrt{2}$-2)2=16-8$\sqrt{2}$.
故答案为:16-8$\sqrt{2}$.
点评 考查了勾股定理,中垂线的性质,等腰直角三角形的判定和性质,本题关键是作出辅助线构造直角三角形,难度较大.

练习册系列答案
相关题目
13.在平面直角坐标系内,点P(-3,2)关于原点的对称点Q的坐标为( )
| A. | (2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
8. OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
 OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )| A. | 80° | B. | 40° | C. | 50° | D. | 20° |
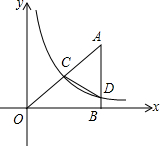 如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.
如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.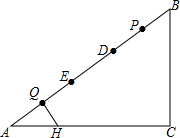 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.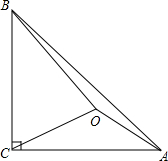 如图,等腰Rt△ABC,∠ACB=90°,OA=1,OC=2,OB=3,求∠AOC的角度.
如图,等腰Rt△ABC,∠ACB=90°,OA=1,OC=2,OB=3,求∠AOC的角度. 如图,?ABCD的对角线AC、BD交于点O,E、G在直线AC上,AE=CG,F、H直线BD上,BF=DH,求证:EF=HG.
如图,?ABCD的对角线AC、BD交于点O,E、G在直线AC上,AE=CG,F、H直线BD上,BF=DH,求证:EF=HG.