题目内容
17．在$\frac{1}{x}$，$\frac{1}{2}$，$\frac{{x}^{2}+1}{2}$，$\frac{3xy}{7}$，$\frac{3}{x+y}$，x+$\frac{1}{y}$中分式的个数有（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
分析 利用分式的定义判断即可．
解答 解：各式中分式有：$\frac{1}{x}$，$\frac{3}{x+y}$，x+$\frac{1}{y}$，共有3个，
故选B
点评 此题考查了分式的定义，熟练掌握分式的定义是解本题的关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8．
OA，OB是⊙O的两条半径，且∠C=40°，点C在⊙O上，则∠AOB的度数为（ ）
OA，OB是⊙O的两条半径，且∠C=40°，点C在⊙O上，则∠AOB的度数为（ ）| A． | 80° | B． | 40° | C． | 50° | D． | 20° |
5．下列方程中，是一元一次方程的是（ ）
| A． | x+4y=1 | B． | x2-2x=3 | C． | 2x-$\frac{x}{3}$=1-$\frac{3x}{2}$ | D． | xy+6=3z |
9．当x=1时，下列各式的值为0的是（ ）
| A． | $\frac{x-1}{{{x^2}-3x+2}}$ | B． | $\frac{1}{x+1}$ | C． | $\frac{2x-2}{x-2}$ | D． | $\frac{x+2}{x-1}$ |
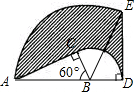如图，△ABC中，∠C是直角，AB=6cm，∠ABC=60°，将△ABC以点B为中心顺时针旋转，使点C旋转到AB边延长线上的D处，则AC边扫过的图形众人阴影部分的面积是9π．