题目内容
16.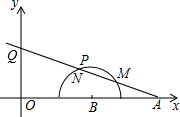 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | $\frac{8}{15}$$\sqrt{3}$ | C. | 2-$\frac{4}{5}$$\sqrt{3}$ | D. | 2$\sqrt{3}$-2 |
分析 延长AN交y轴于Q1,延长AM交y轴于Q2,作NE⊥OA于E,由NE∥OQ1,得$\frac{NE}{O{Q}_{1}}=\frac{AE}{AO}$求出OQ1,再证明∠BAM=30°,在RT△OAQ2中求出OQ2即可求出Q1Q2.
解答 解:如图延长AN交y轴于Q1,延长AM交y轴于Q2,作NE⊥OA于E,
∵M、N是半圆的三等分点,
∴∠NBO=∠MBN=∠MBA=60°,
在RT△BNE中,∵BN=1,∠NBE=60°,
∴∠BNE=30°,EB=$\frac{1}{2}$BN=$\frac{1}{2}$,NE=$\sqrt{3}$EB=$\frac{\sqrt{3}}{2}$,
∵NE∥OQ1,
∴$\frac{NE}{O{Q}_{1}}=\frac{AE}{AO}$,
∴$\frac{\frac{\sqrt{3}}{2}}{O{Q}_{1}}=\frac{\frac{5}{2}}{4}$,
∴OQ1=$\frac{4\sqrt{3}}{5}$,
∵BM=BG,∠MBG=60°,
∴△MBG是等边三角形,
∴MG=BM=AG,
∴∠AMB=90°,∠MAB=30°,
在RT△AOQ2中,∵AO=4,∠OAQ2=30°,
∴OQ2=$\frac{\sqrt{3}}{3}$OA=$\frac{4\sqrt{3}}{3}$,
∴Q1Q2=OQ2-OQ1=$\frac{8\sqrt{3}}{15}$.
故选B.
点评 本题考查轨迹的有关知识、直角三角形30度角的性质、平行线分线段成比例定理等知识,解轨迹题目的关键是找到起始点和终点的位置,确定轨迹的图形.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.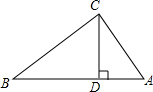 如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
 如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )| A. | 1.6 | B. | 2.4 | C. | 2 | D. | 2.1 |
8. OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
 OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )| A. | 80° | B. | 40° | C. | 50° | D. | 20° |
5.下列方程中,是一元一次方程的是( )
| A. | x+4y=1 | B. | x2-2x=3 | C. | 2x-$\frac{x}{3}$=1-$\frac{3x}{2}$ | D. | xy+6=3z |
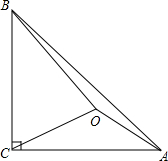 如图,等腰Rt△ABC,∠ACB=90°,OA=1,OC=2,OB=3,求∠AOC的角度.
如图,等腰Rt△ABC,∠ACB=90°,OA=1,OC=2,OB=3,求∠AOC的角度. 如图,在△ABC中,点D,E分别是AC,AB上的两点,且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.
如图,在△ABC中,点D,E分别是AC,AB上的两点,且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.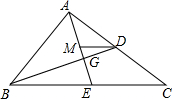 如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.
如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.