题目内容
7.(1)操作发现:如图①,在Rt△ABC中,∠C=2∠B=90°,点D是BC上一点,沿AD折叠△ADC,使得点C恰好落在AB上的点E处,请写出AB、AC、CD之间的关系AB=AC+DC
(2)问题解决:
如图②,若(1)中∠C≠90°,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
(3)类比探究:
如图③,在四边形ABCD中,∠B=120°,∠D=90°,AB=BC,AD=DC,连接AC,点E是CD上一点,沿AE折叠,使得点D正好落在AC上的点F处,若BC=3,直接写出DE的长.
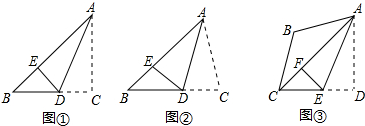
分析 (1)由翻折的性质可知:AE=AC,DE=DC,然后证明△BED为等腰直角三角形,从而得到BE=ED,故此可证得AB=AC+CD;
(2)由翻折的性质得到AE=AC,DE=DC,∠C=∠AED,由三角形外角的性质可证明∠B=∠EDB,从而得到BE=ED,于是可证明AB=AC+CD;
(3)过点B作BH⊥AC,垂足为H,由特殊锐角三角函数值可知CH的长,从而得到AC的长,然后求得AD的长,最后根据AC=AD+DE求解即可.
解答 解:(1)∵∠C=2∠B=90°,
∴∠B=45°.
由翻折的性质可知:AE=AC,DE=DC,∠C=∠AED=90°.
∵∠B=45°,∠BED=90°,
∴∠EDB=45°.
∴∠B=∠EDB=45°.
∴BE=ED.
∴BE=DC.
∴AB=AC+DC.
故答案为:AB=AC+DC.
(2)由翻折的性质可知:AE=AC,DE=DC,∠C=∠AED.
∵∠B+∠EDB=∠AED,∠C=2∠B,
∴∠B=∠BDE.
∴BE=ED.
∴BE=DC.
∴AB=AC+DC.
(3)如图所示:过点B作BH⊥AC,垂足为H.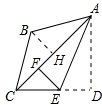
∵∠B=120°,AB=BC,
∴∠BCA=∠BAC=30°.
∴CH=BC×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
∵AB=BC,BH⊥AC,
∴CH=HA.
∴AC=3$\sqrt{3}$.
在Rt△ACD中,AD=$3\sqrt{3}×\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{6}}{2}$.
∵AC=AD+ED,
∴ED=AC-AD=3$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$=$\frac{6\sqrt{3}-3\sqrt{6}}{2}$.
点评 本题主要考查的是翻折的性质、三角形外角的性质、等腰三角形三线合一的性质、特殊锐角三角函数值的应用,证得BE=ED是解题的关键.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | x=y | B. | -mx=my | C. | mx+1=my-1 | D. | 9-mx=9-my |
 如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.
如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.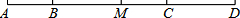 如图,已知B、C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
如图,已知B、C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.