题目内容
2.x取何值时,下列分式有意义:(1)$\frac{x+2}{2x-3}$
(2)$\frac{6(x+3)}{|x|-12}$
(3)$\frac{x+6}{{{x^2}+1}}$.
分析 (1)根据分式的分母不为零分式有意义,可得答案;
(2)根据分式的分母不为零分式有意义,可得答案;
(3)根据分式的分母不为零分式有意义,可得答案.
解答 解:(1)要使$\frac{x+2}{2x-3}$有意义,
得2x-3≠0.
解得x≠$\frac{3}{2}$,
当x≠$\frac{3}{2}$时,$\frac{x+2}{2x-3}$有意义;
(2)要使$\frac{6(x+3)}{|x|-12}$有意义,得
|x|-12≠0.
解得x≠±12,
当x≠±12时,$\frac{6(x+3)}{|x|-12}$有意义;
(3)要使$\frac{x+6}{{{x^2}+1}}$有意义,得
x2+1≠0.
x为任意实数,$\frac{x+6}{{{x^2}+1}}$有意义.
点评 本题考查了分式有意义,分式的分母不为零分式有意义.

练习册系列答案
相关题目
12.某品牌电视机连续两次降价20%后,又再降价10%,或者连续两次降价25%,则前者的售价比后者的售价( )
| A. | 少2% | B. | 不多也不少 | C. | 多5% | D. | 多1.35% |
10. 如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 茶 | D. | 城 |
 如图,点C,D在线段AB上,△PCD是等边三角形,且∠APB=120°,求证:
如图,点C,D在线段AB上,△PCD是等边三角形,且∠APB=120°,求证: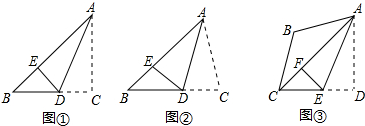
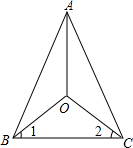 已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,求证:
已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,求证: 在△ABC中,AB=AC,AC边上的中线BD把三角形ABC的周长分为9cm和12cm的两部分,求三角形各边的长.
在△ABC中,AB=AC,AC边上的中线BD把三角形ABC的周长分为9cm和12cm的两部分,求三角形各边的长.