题目内容
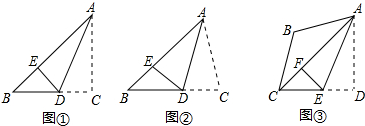
5.小明将一张长方形纸片分别折叠出如图所示的图形,让小亮仔细观察重叠部分的图形特点,并解决下列问题.
(1)观察如中a,b,c,d中∠1和∠2的关系,并说明理由;
(2)猜想图c中△MBD是什么形状的三角形(按边),并说明理由;
(3)如图d中∠1=60°,猜想△MEF是什么形状的三角形(按边),并说明理由.
分析 (1)由折叠的性质容易得出结论;
(2)由折叠的性质得出∠1=∠2,由平行线的性质得出∠MDB=∠1,得出∠MDB=∠2,由等角对等边得出MB=MD即可;
(3)由折叠的性质得出∠2=∠1=60°,由(2)得出△MEF是等腰三角形,即可得出结论.
解答 解:(1)图a,b,c,d中∠1=∠2;理由如下:
由折叠的性质得:∠1=∠2;
(2)△MBD是等腰三角形;理由如下:
由折叠的性质得:∠1=∠2,
∵AD∥BC,
∴∠MDB=∠1,
∴∠MDB=∠2,
∴MB=MD,
∴△MBD是等腰三角形;
(3)△MEF是等边三角形,理由如下:
由折叠的性质得:∠2=∠1=60°,
由(2)得:△MEF是等腰三角形,
故△MEF是等边三角形.
点评 本题考查了翻折变换的性质、等腰三角形的判定、平行线的性质、等边三角形的判定;熟练掌握翻折变换的性质,弄清角之间的数量关系是解决问题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
8.某工厂安排20名技工组装A、B、C三个型号的玩具,按规定每天共组装420件玩具,每名技工只组装同一型号的玩具,且至少有2名技工组装同一个型号的玩具.
(1)设工厂安排x名技工组装A型玩具,y名技工组装B型玩具,根据上表提供的信息,求x与y之间的函数关系式,并求出x的取值范围.
(2)工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
| 玩具型号 | A型 | B型 | C型 |
| 每名技工每天组装的数量(个) | 22 | 21 | 20 |
| 每件玩具获得的利润(元) | 8 | 10 | 6 |
(2)工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
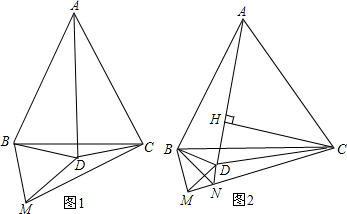
 在△ABC中,AB=AC,AC边上的中线BD把三角形ABC的周长分为9cm和12cm的两部分,求三角形各边的长.
在△ABC中,AB=AC,AC边上的中线BD把三角形ABC的周长分为9cm和12cm的两部分,求三角形各边的长.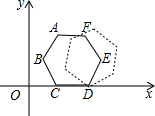 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.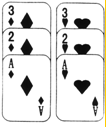 如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)
如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)