题目内容
19.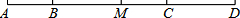 如图,已知B、C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
如图,已知B、C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
分析 由题意得AB=$\frac{1}{5}$AD,由中点的定义可知AM=$\frac{1}{2}AD$,从而可得到$\frac{1}{2}AD-\frac{1}{5}AD$=6,从而可求得AD的长,然后由MD=$\frac{1}{2}AD$,CD=$\frac{3}{10}$AD,根据CM=MD-CD可求得CM的长.
解答 解:∵B、C两点把线段AD分成2:5:3三部分,
∴AB=$\frac{1}{5}$AD,CD=$\frac{3}{10}$AD.
∵M为AD的中点,
∴AM=$\frac{1}{2}AD$.
∵BM=AM-AB,
∴$\frac{1}{2}AD-\frac{1}{5}AD$=6.
解得:AD=20cm.
∴CD=$\frac{3}{10}×20=6$cm.
∵M为AD的中点,
∴MD=$\frac{1}{2}×20$=10cm.
∴CM=MD-CD=10-6=4cm.
点评 本题主要考查的是两点间的距离,根据BM=6cm列出关于AD的方程是解题的关键.

练习册系列答案
相关题目
10. 如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“中”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 茶 | D. | 城 |
8.某工厂安排20名技工组装A、B、C三个型号的玩具,按规定每天共组装420件玩具,每名技工只组装同一型号的玩具,且至少有2名技工组装同一个型号的玩具.
(1)设工厂安排x名技工组装A型玩具,y名技工组装B型玩具,根据上表提供的信息,求x与y之间的函数关系式,并求出x的取值范围.
(2)工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
| 玩具型号 | A型 | B型 | C型 |
| 每名技工每天组装的数量(个) | 22 | 21 | 20 |
| 每件玩具获得的利润(元) | 8 | 10 | 6 |
(2)工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
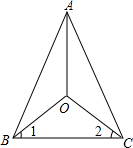 已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,求证:
已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,求证: