题目内容
12．一个直角三角形的斜边长为2，一条直角边长为$\sqrt{2}$，则另一条直角边长是（ ）| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | 3 |
分析 根据勾股定理即可求得另一条直角边的长．
解答 解：由勾股定理得：另一直角边=$\sqrt{{2}^{2}-（\sqrt{2}）^{2}}$=$\sqrt{2}$，
故选：C．
点评 本题考查了利用勾股定理解直角三角形的能力即：直角三角形两直角边的平方和等于斜边的平方．
练习册系列答案
相关题目
2．下列命题中：
①同位角相等，两直线平行；
②在△ABC中，a，b，c分别是∠A、∠B、∠C的对边，如果∠C=90°，那么a2+b2=c2；
③菱形是对角线互相垂直的四边形；
④矩形是对角线相等的平行四边形．
它们的逆命题是真命题的有（ ）
①同位角相等，两直线平行；
②在△ABC中，a，b，c分别是∠A、∠B、∠C的对边，如果∠C=90°，那么a2+b2=c2；
③菱形是对角线互相垂直的四边形；
④矩形是对角线相等的平行四边形．
它们的逆命题是真命题的有（ ）
| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
3．命题：“关于x的一元二次方程x2+bx+1=0，当b＜0时，必有实数根”；能说明这个命题是假命题的一个反例可以是（ ）
| A． | b=-1 | B． | b=-2 | C． | b=-3 | D． | b=-4 |
20．$\sqrt{3}tan（α+2{0°}）=1$，锐角α的度数应是（ ）
| A． | 40° | B． | 30° | C． | 20° | D． | 10° |
7．
如图，AB∥EF∥CD，EG∥BD，则图中与∠1相等的角共有（ ）
如图，AB∥EF∥CD，EG∥BD，则图中与∠1相等的角共有（ ）| A． | 6个 | B． | 5个 | C． | 4个 | D． | 3个 |
17．
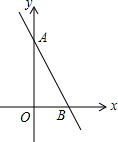如图，若一次函数y=-2x+b的图象交y轴于点A（0，3），则不等式-2x+b＞0的解集为（ ）
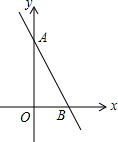如图，若一次函数y=-2x+b的图象交y轴于点A（0，3），则不等式-2x+b＞0的解集为（ ）| A． | x＞$\frac{3}{2}$ | B． | x＞3 | C． | x＜$\frac{3}{2}$ | D． | x＜3 |
4．若五个正整数的中位数是3，且唯一的众数是7，则这五个数的平均数是（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 8 |
1．如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（ ）
| A． | 7，24，25 | B． | 3，4，$\frac{14}{3}$ | C． | 3，4，5 | D． | 15，8，17 |
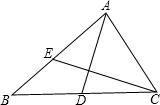如图，D、E分别是△ABC的边BC和AB上的点，△ABD与△ACD的周长相等，△CAE与△CBE的周长相等，设BC=a，AC=b，AB=c，给出以下几个结论：