题目内容
3.命题:“关于x的一元二次方程x2+bx+1=0,当b<0时,必有实数根”;能说明这个命题是假命题的一个反例可以是( )| A. | b=-1 | B. | b=-2 | C. | b=-3 | D. | b=-4 |
分析 先根据判别式得到△=b2-4,在满足b<0的前提下,取b=-1得到△<0,根据判别式的意义得到方程没有实数解,于是b=-1可作为说明这个命题是假命题的一个反例.
解答 解:△=b2-4,由于当b=-1时,满足b<0,而△<0,方程没有实数解,所以当b=-1时,可说明这个命题是假命题.
故选A.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了根的判别式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
14.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
18.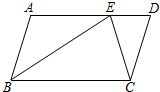 如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
 如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )| A. | 5 | B. | 4 | C. | 3.6 | D. | 3 |
8.不等式2x-1≤4的最大整数解是( )
| A. | 0 | B. | 1 | C. | $\frac{5}{2}$ | D. | 2 |
15.若函数y=kx+2的图象经过点(1,3),则当y=0时,x=( )
| A. | -2 | B. | 2 | C. | 0 | D. | ±2 |
12.一个直角三角形的斜边长为2,一条直角边长为$\sqrt{2}$,则另一条直角边长是( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
13.在平面直角坐标系中,点A位于第一象限,则点A的坐标可以为( )
| A. | (1,4) | B. | (-4,1) | C. | (-1,-4) | D. | (4,-1) |
