题目内容
4．若五个正整数的中位数是3，且唯一的众数是7，则这五个数的平均数是（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 8 |
分析 首先根据众数与中位数的定义，得出这五个数据中的三个数，再根据一组数据由五个正整数组成，得出其它两个数，最后由平均数的意义得出结果．
解答 解：∵五个正整数的中位数是3，唯一的众数是7，
∴知道的三个数是3，7，7；
∵一组数据由五个正整数组成，
∴另两个为1，2；
∴这五个正整数的平均数是（1+2+3+7+7）÷5=4；
故选A．
点评 本题考查了平均数、众数与中位数的意义，掌握平均数、众数与中位数的计算公式是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
14．下列根式中，与$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{8}$ | C． | $\sqrt{6}$ | D． | $\sqrt{3}$ |
15．若函数y=kx+2的图象经过点（1，3），则当y=0时，x=（ ）
| A． | -2 | B． | 2 | C． | 0 | D． | ±2 |
12．一个直角三角形的斜边长为2，一条直角边长为$\sqrt{2}$，则另一条直角边长是（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | 3 |
19．下列说法正确的是（ ）
| A． | -2是4的平方根 | B． | 4的平方根是2 | C． | 2没有平方根 | D． | $\root{3}{3}$大于$\frac{3}{2}$ |
9．
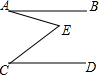如图，AB∥CD，则∠BAE，∠AEC，∠ECD三个角之间的关系为（ ）
如图，AB∥CD，则∠BAE，∠AEC，∠ECD三个角之间的关系为（ ）| A． | ∠BAE=∠AEC+∠ECD | B． | ∠BAE=∠AEC-∠ECD | C． | ∠BAE=∠ECD-∠AEC | D． | 不能确定 |
16．某反比例函数的图象经过点（-2，3），则该图象一定不经过点（ ）
| A． | （1，6） | B． | （-1，6） | C． | （2，-3） | D． | （3，-2） |
13．在平面直角坐标系中，点A位于第一象限，则点A的坐标可以为（ ）
| A． | （1，4） | B． | （-4，1） | C． | （-1，-4） | D． | （4，-1） |
5．
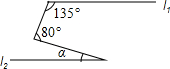如图直线l1∥l2，则∠α的大小（ ）
如图直线l1∥l2，则∠α的大小（ ）| A． | 35° | B． | 45° | C． | 55° | D． | 80° |