��Ŀ����
13��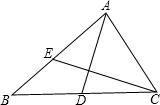 ��ͼ��D��E�ֱ��ǡ�ABC�ı�BC��AB�ϵĵ㣬��ABD���ACD���ܳ���ȣ���CAE���CBE���ܳ���ȣ���BC=a��AC=b��AB=c���������¼������ۣ�
��ͼ��D��E�ֱ��ǡ�ABC�ı�BC��AB�ϵĵ㣬��ABD���ACD���ܳ���ȣ���CAE���CBE���ܳ���ȣ���BC=a��AC=b��AB=c���������¼������ۣ������AD��BC�����ߣ���ôCE��AB�����ߣ�
��AE�ij���Ϊ$\frac{c+a-b}{2}$��
��BD�ij���Ϊ$\frac{b+a-c}{2}$��
������BAC=90�㣬��ABC�����ΪS����S=AE•BD��
������ȷ�Ľ����Ǣڢۢܣ�����ȷ���۵���Ŷ����ϣ�
���� �����ߵĶ��壬�ɵõ�AB=AC����AB=ACʱδ����AC=BC�����жϢ٣���ABD���ACD���ܳ���ȣ����ǿɵó���AB+BD=AC+CD����ʽ�����ұ�������������ABC�ܳ���һ�룬��AB��AC��ֵ����ô�������BD�ij��ˣ�ͬ�������AE�ij������жϢڢۣ���AE��BD������㣬��Ϲ��ɶ��������S�����жϢܣ���ɵó��𰸣�
��� �⣺
��AD��BC������ʱ����BD=CD��
�ߡ�ABD���ACD���ܳ���ȣ�
��AB=AC��
����ʱ�����ܵó�AC=BC�������ܵó�CE��AB�����ߣ�
�ʢٲ���ȷ��
�ߡ�ABD���ACD���ܳ���ȣ�BC=a��AC=b��AB=c��
��AB+BD+AD=AC+CD+AD��
��AB+BD=AC+CD��
��AB+BD+CD+AC=a+b+c��
��AB+BD=AC+CD=$\frac{a+b+c}{2}$��
��BD=$\frac{a+b+c}{2}$-c=$\frac{a+b-c}{2}$��
ͬ��AE=$\frac{a+c-b}{2}$��
�ʢڢ۶���ȷ��
����BAC=90��ʱ����b2+c2=a2��
��AE•BE=$\frac{a+c-b}{2}$��$\frac{a+b-c}{2}$=$\frac{1}{4}$[a-��c-b��][a-��c-b��]=$\frac{1}{4}$[a2-��c-b��2]=$\frac{1}{4}$[a2-��c2+b2-2bc��]=$\frac{1}{4}$��2bc=$\frac{1}{2}$bc=S��
�ʢ���ȷ��
���Ͽ�֪��ȷ�Ľ��ۢڢۢܣ�
�ʴ�Ϊ���ڢۢܣ�
���� ����Ϊ�����ε��ۺ�Ӧ�ã���Ҫ�����������θ���֮��Ĺ�ϵ���⼰�����ε����������ʽ�ӵ�ʱ��Ҫע���ҳ�������ϵ���Ѷ����У�

| A�� | 1 | B�� | 2 | C�� | $\sqrt{2}$ | D�� | 3 |
| A�� | ��1��4�� | B�� | ��-4��1�� | C�� | ��-1��-4�� | D�� | ��4��-1�� |
��${��{-\frac{1}{2}}��^{-3}}=-\frac{1}{8}$����a2+2a-1=��a-1��2����a8��a8=1��a��0�����ܣ�a-b��2=a2-b2��
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
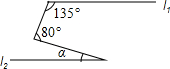 ��ͼֱ��l1��l2����Ϧ��Ĵ�С��������
��ͼֱ��l1��l2����Ϧ��Ĵ�С��������| A�� | 35�� | B�� | 45�� | C�� | 55�� | D�� | 80�� |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | -2 |
| A�� | y=-��x-2��2-1 | B�� | y=-��x-2��2+1 | C�� | y=-��x+2��2+1 | D�� | y=-��x+2��2-1 |
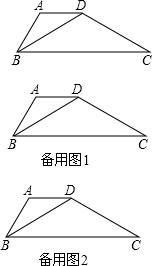 ��ͼ��������ֽƬABCD�У�AD��BC��AD=AB=4��BD=CD����C=30�㣬EΪBC����һ�㣬��BEΪֱ�DZߣ�EΪֱ�Ƕ���������Rt��BEF��ʹ����Rt��BEF������ABCD��BC��ͬ�࣮
��ͼ��������ֽƬABCD�У�AD��BC��AD=AB=4��BD=CD����C=30�㣬EΪBC����һ�㣬��BEΪֱ�DZߣ�EΪֱ�Ƕ���������Rt��BEF��ʹ����Rt��BEF������ABCD��BC��ͬ�࣮