题目内容
20．$\sqrt{3}tan（α+2{0°}）=1$，锐角α的度数应是（ ）| A． | 40° | B． | 30° | C． | 20° | D． | 10° |
分析 结合特殊角的三角函数值求解即可．
解答 解：∵$\sqrt{3}$tan（α+20°）=1，
∴tan（α+20°）=$\frac{\sqrt{3}}{3}$，
又∵∠α为锐角，
∴∠α=10°．
故选D．
点评 本题考查了特殊角的三角函数值，解答本题的关键在于熟练掌握各特殊角的三角函数值．
练习册系列答案
相关题目
10．下列命题中，假命题是（ ）
| A． | 有两角和其中一角的对边对应相等的两个三角形全等 | |
| B． | 面积相等的两个三角形全等 | |
| C． | 有一边相等的两个等边三角形全等 | |
| D． | 三边对应相等的两个三角形全等 |
8．不等式2x-1≤4的最大整数解是（ ）
| A． | 0 | B． | 1 | C． | $\frac{5}{2}$ | D． | 2 |
15．若函数y=kx+2的图象经过点（1，3），则当y=0时，x=（ ）
| A． | -2 | B． | 2 | C． | 0 | D． | ±2 |
5．
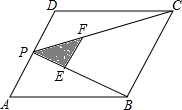如图，P为平行四边形ABCD边AD上一点，E、F分别是PB、PC（靠近点P）的三等分点，△PEF、△PDC、△PAB的面积分别为S1、S2、S3，若AD=2，AB=2$\sqrt{3}$，∠A=60°，则S1+S2+S3的值为（ ）
如图，P为平行四边形ABCD边AD上一点，E、F分别是PB、PC（靠近点P）的三等分点，△PEF、△PDC、△PAB的面积分别为S1、S2、S3，若AD=2，AB=2$\sqrt{3}$，∠A=60°，则S1+S2+S3的值为（ ）| A． | $\frac{10}{3}$ | B． | $\frac{9}{2}$ | C． | $\frac{13}{3}$ | D． | 4 |
12．一个直角三角形的斜边长为2，一条直角边长为$\sqrt{2}$，则另一条直角边长是（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | 3 |
9．
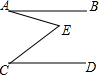如图，AB∥CD，则∠BAE，∠AEC，∠ECD三个角之间的关系为（ ）
如图，AB∥CD，则∠BAE，∠AEC，∠ECD三个角之间的关系为（ ）| A． | ∠BAE=∠AEC+∠ECD | B． | ∠BAE=∠AEC-∠ECD | C． | ∠BAE=∠ECD-∠AEC | D． | 不能确定 |
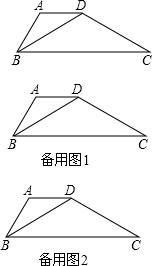如图，在梯形纸片ABCD中，AD∥BC，AD=AB=4，BD=CD，∠C=30°，E为BC边上一点，以BE为直角边，E为直角顶点作等腰Rt△BEF，使等腰Rt△BEF和梯形ABCD在BC的同侧．