题目内容
17.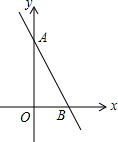 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )| A. | x>$\frac{3}{2}$ | B. | x>3 | C. | x<$\frac{3}{2}$ | D. | x<3 |
分析 根据点A的坐标找出b值,令一次函数解析式中y=0求出x值,从而找出点B的坐标,观察函数图象,找出在x轴上方的函数图象,由此即可得出结论.
解答 解:∵一次函数y=-2x+b的图象交y轴于点A(0,3),
∴b=3,
令y=-2x+3中y=0,则-2x+3=0,解得:x=$\frac{3}{2}$,
∴点B($\frac{3}{2}$,0).
观察函数图象,发现:
当x<$\frac{3}{2}$时,一次函数图象在x轴上方,
∴不等式-2x+b>0的解集为x<$\frac{3}{2}$.
故选C.
点评 本题考查了一次函数与一元一次不等式,解题的关键是找出交点B的坐标.本题属于基础题,难度不大,解决该题型题目时,根据函数图象的上下位置关系解不等式是关键.

练习册系列答案
相关题目
7. 如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )
如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )
 如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )
如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )| A. | ASA | B. | SAS | C. | SSS | D. | AAS |
8.不等式2x-1≤4的最大整数解是( )
| A. | 0 | B. | 1 | C. | $\frac{5}{2}$ | D. | 2 |
5.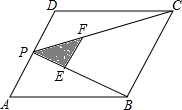 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )| A. | $\frac{10}{3}$ | B. | $\frac{9}{2}$ | C. | $\frac{13}{3}$ | D. | 4 |
12.一个直角三角形的斜边长为2,一条直角边长为$\sqrt{2}$,则另一条直角边长是( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
2. 将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )
将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )
 将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )
将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
9.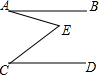 如图,AB∥CD,则∠BAE,∠AEC,∠ECD三个角之间的关系为( )
如图,AB∥CD,则∠BAE,∠AEC,∠ECD三个角之间的关系为( )
 如图,AB∥CD,则∠BAE,∠AEC,∠ECD三个角之间的关系为( )
如图,AB∥CD,则∠BAE,∠AEC,∠ECD三个角之间的关系为( )| A. | ∠BAE=∠AEC+∠ECD | B. | ∠BAE=∠AEC-∠ECD | C. | ∠BAE=∠ECD-∠AEC | D. | 不能确定 |
6.下列图案中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |