题目内容
7.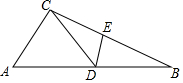 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为60°.
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为60°.
分析 根据等腰三角形的性质推出∠A=∠CDA=40°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=20°,由三角形的内角和定理求出∠BDE,根据平角的定义即可求出选项.
解答 解:∵AC=CD=BD=BE,∠A=40°,
∴∠A=∠CDA=40°,∠B=∠DCB,∠BDE=∠BED,
∵∠B+∠DCB=∠CDA=40°,
∴∠B=20°,
∵∠B+∠EDB+∠DEB=180°,
∴∠BDE=∠BED=$\frac{1}{2}$(180°-20°)=80°,
∴∠CDE=180°-∠CDA-∠EDB=180°-40°-80°=60°,
故答案为:60°
点评 本题主要考查对等腰三角形的性质,三角形的内角和定理,三角形的外角性质,邻补角的定义等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知三角形的两边长分别为3cm和7cm,则该三角形的第三边的长可能是( )
| A. | 2cm | B. | 3cm | C. | 9cm | D. | 10cm |
17. 按如下方法,将△ABC的三边缩小的原来的$\frac{1}{2}$,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的是( )
按如下方法,将△ABC的三边缩小的原来的$\frac{1}{2}$,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的是( )
 按如下方法,将△ABC的三边缩小的原来的$\frac{1}{2}$,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的是( )
按如下方法,将△ABC的三边缩小的原来的$\frac{1}{2}$,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的是( )| A. | △ABC与△DEF不是位似图形 | B. | $\frac{OE}{OB}$=$\frac{1}{3}$ | ||
| C. | △ABC与△DEF的周长比为1:2 | D. | △ABC与△DEF的面积比为4:1 |
 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{-2}{x}$的图象交于A(-1,m),B(n,-1)两点.
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{-2}{x}$的图象交于A(-1,m),B(n,-1)两点. 如图,在△ABC中,AB=AC,∠BAC=120°,过点A作AB的垂线交BC于D,BC=6,则AD的长为( )
如图,在△ABC中,AB=AC,∠BAC=120°,过点A作AB的垂线交BC于D,BC=6,则AD的长为( )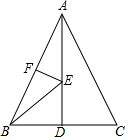 如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )
如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )