题目内容
15. 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{-2}{x}$的图象交于A(-1,m),B(n,-1)两点.
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{-2}{x}$的图象交于A(-1,m),B(n,-1)两点.(1)若C(x1,y1),D(x2,y2)是反比例函数的图象上的两点,且0<x1<x2,试比较y1,y2的大小得y1< y2;
(2)求这个一次函数点的表达式.
分析 (1)根据反比例函数的性质即可直接判断;
(2)首先把A和B的坐标代入反比例函数解析式求得m和n的值,然后利用待定系数法求得函数解析式.
解答 解:(1)∵比例系数k=-2<0,
∴当且0<x1<x2时,y1<y2.
故答案是:<;
(2)把A(-1,m)和B(n,-1)代入y=-$\frac{-2}{x}$得:m=2,n=2.
则A的坐标是(-1,2),B的坐标是(2,-1).
根据题意得$\left\{\begin{array}{l}{-k+b=2}\\{2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
则一次函数的解析式是y=-x+1.
点评 本题考查了待定系数法求函数的解析式,以及反比例函数的性质,正确求得m和n的值是关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
5. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )| A. | 52° | B. | 60° | C. | 62° | D. | 72° |
6.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
20.抛物线y=ax2+bx+c(a≠0)部分点的横坐标x,纵坐标y的对应值如下表
从上表可知,下列说法错误的是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 抛物线与x轴的一个交点坐标为(3,0) | B. | 函数y=ax2+bx+c的最大值为6 | ||
| C. | 抛物线的对称轴是直线x=$\frac{1}{2}$ | D. | 在对称轴左侧,y随x增大而增大 |
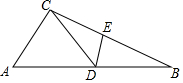 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为60°.
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为60°.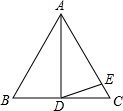 如图,AD是等边三角形ABC的中线,E是AC上的一点,且AE=AD,求∠EDC的度数.
如图,AD是等边三角形ABC的中线,E是AC上的一点,且AE=AD,求∠EDC的度数. 如图,已知O是∠PAB的一边AB上的点,按要求作图:
如图,已知O是∠PAB的一边AB上的点,按要求作图: