题目内容
16.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD边上的高为5,求BD的长.
分析 (1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BED=∠ABE+∠BAD,然后代入数据计算即可得解;
(2)根据三角形的中线把三角形分成两个面积相等的三角形求出△BDE的面积,分三种情况讨论,根据三角形的面积公式列式计算即可得解.
解答 解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD.
又∠ABE=15°,∠BAD=40°,
∴∠BED=55°.
(2)∵AD为△ABC的中线,
∴${S}_{△ABD}={S}_{△ACD}=\frac{1}{2}{S}_{ABC}$=20,
BD边上的高为5,
①当△ABD中BD边上的高是5,
∴S△ABD=$\frac{1}{2}$BD×5=20,
∴BD=8,
②当△BDE的边BD上的高为5,
∵BE是△ABD的中线,
∴S△BDE=$\frac{1}{2}$S△ABD=10,
∴S△BDE=$\frac{1}{2}$BD×5=10,
∴BD=4,
即:满足条件的BD是4或8.
点评 本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的面积,(2)根据等底等高的三角形的面积相等得到三角形的中线把三角形分成两个面积相等的三角形求出△BDE的面积是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
6. 如图,已知∠B=42°,∠BDE=138°,则( )
如图,已知∠B=42°,∠BDE=138°,则( )
 如图,已知∠B=42°,∠BDE=138°,则( )
如图,已知∠B=42°,∠BDE=138°,则( )| A. | EF∥BC | B. | ED∥AB | C. | DF∥AC | D. | 以上都不对 |
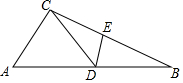 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为60°.
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为60°.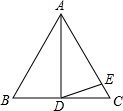 如图,AD是等边三角形ABC的中线,E是AC上的一点,且AE=AD,求∠EDC的度数.
如图,AD是等边三角形ABC的中线,E是AC上的一点,且AE=AD,求∠EDC的度数. 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c. 如图,已知O是∠PAB的一边AB上的点,按要求作图:
如图,已知O是∠PAB的一边AB上的点,按要求作图: