题目内容
17.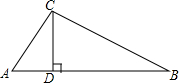 如图所示,在△ABC中,∠A为锐角,CD为AB边上的高,$\frac{CD}{AC}$=$\frac{3}{5}$,AB+AC=6,设AC=x,△ABC的面积为y.
如图所示,在△ABC中,∠A为锐角,CD为AB边上的高,$\frac{CD}{AC}$=$\frac{3}{5}$,AB+AC=6,设AC=x,△ABC的面积为y.(1)求y关于x的函数关系式和自变量x的取值范围;
(2)当AC长度为何值时,△ABC的面积最大?
分析 (1)由$\frac{CD}{AC}$=$\frac{3}{5}$,AC=x,求得CD=$\frac{3x}{5}$,由AB+AC=6,AC=x,求得AB=6-x,然后根据三角形的面积公式即可得到结果;
(2)根据y=-$\frac{3}{10}{x}^{2}$+$\frac{9}{5}$x=-$\frac{3}{10}$(x-3)2+$\frac{27}{10}$,即可得到结论.
解答 解:(1)∵$\frac{CD}{AC}$=$\frac{3}{5}$,AC=x,
∴CD=$\frac{3x}{5}$,
∵AB+AC=6,AC=x,
∴AB=6-x,
∴y=$\frac{1}{2}$AB•CD=$\frac{1}{2}$(6-x)×$\frac{3x}{5}$,
∴y=-$\frac{3}{10}{x}^{2}$+$\frac{9}{5}$x,(0<x<6);
(2)∵y=-$\frac{3}{10}{x}^{2}$+$\frac{9}{5}$x=-$\frac{3}{10}$(x-3)2+$\frac{27}{10}$,
∴当x=3时,y最大值=$\frac{27}{10}$,
即:当AC=3时,△ABC的面积最大.
点评 本题考查了三角形的面积,二次函数的最值,熟记三角形的面积公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.一条直线y=kx+b经过第二、三、四象限,则下列所给数据符合题意的是( )
| A. | k+b=6,kb=-5 | B. | k+b=-5,kb=-6 | C. | k+b=6,kb=5 | D. | k+b=-5,kb=6 |
2.已知一个物体由x个相同的正方体堆成,它的主视图和左视图如图所示,那么x的最小值是( )


| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
7.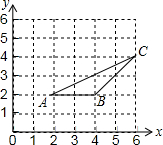 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )| A. | (2,$\frac{3}{2}$) | B. | (-2,-$\frac{3}{2}$) | C. | (2,$\frac{3}{2}$)或(-2,-$\frac{3}{2}$) | D. | (8,6)或(-8,-6) |
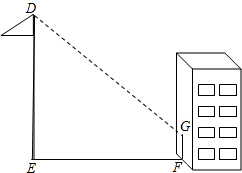 李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.
李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.