题目内容
13.如图,抛物线y=-x2+2x+8交x轴于A、B,直线y=x+m与抛物线交于点A、D,与y轴交于点C,点D纵坐标为5(1)求的m值和△BCD的面积S.
(2)点P为抛物线在第一象限的图象上一点,直线PC交x轴于点E,若PC=3CE,求点P的坐标.
(3)在(2)的条件下,点Q为x轴上一点,把△PCQ沿CQ翻折,点P刚好落在x轴上的点G处,求Q点坐标.

分析 (1)首先根据抛物线的解析式求得点A和点B的坐标,然后将点A代入直线的解析式即可求得m的值,然后根据点D的纵坐标求得点D和点C的坐标,从而求得S;
(2)设P(m,-m2+2m+8),作PH⊥x轴,交x轴于点H,从而得到△EOC∽△EHP,利用相似三角形对应边的比相等得到PH=4OC,从而列出方程-m2+2m+8=4×2,求得m的值即可确定点的坐标;
(3)作PK⊥y轴,从而得到PK=2,KC=8-2=6,然后由翻折得△CQG≌△CQP,从而得到QG=QP,CG=CP=2$\sqrt{10}$,然后在Rt△OCG中求得GO的长即可求得点G的坐标.
解答 解:(1)∵y=-x2+2x+8交x轴于A、B,
∴y=-x2+2x+8=0,
解得:x=-2或x=4,
∴A(-2,0),(4,0),
∵直线y=x+m经过点A,
∴-2+m=0,
解得:m=2,
所以直线的解析式为:y=x+2,
令x=0,得y=2,
∴点C的坐标为(0,2),
∵D的纵坐标为5,
∴5=x+2,
解得:x=3
∴D(3,5),
∴S=S△BAD-S△BAC=$\frac{1}{2}$×6×3-$\frac{1}{2}$×6×2=9-6=3;
(2)设P(m,-m2+2m+8),
作PH⊥x轴,交x轴于点H,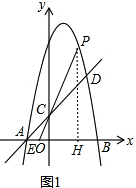
∴CO∥PH,
∴△EOC∽△EHP,
∴$\frac{EC}{EP}=\frac{CO}{PH}$,
∵PC=3CE,
∴$\frac{EC}{EP}=\frac{CO}{PH}=\frac{1}{4}$,
∴PH=4OC,
∴-m2+2m+8=4×2,
解得 m=2,或m=0(舍去),
∴P(2,8);
(3)作PK⊥y轴,
∴PK=2,KC=8-2=6,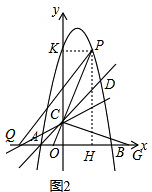
在Rt△CPK中,CP=2$\sqrt{10}$,
由翻折得△CQG≌△CQP,
∴QG=QP,CG=CP=2$\sqrt{10}$,
在Rt△OCG中,
∵CP=2$\sqrt{10}$,OC=2,
∴GO=6,
∴G(6,0)或G(-6,0),
过P作PH⊥x轴,则H(2,0),且PH=8,
设Q(n,0)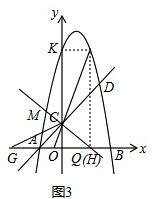
则QP2=PH2+QH2=82+(n-2)2,
GQ=|xQ-xG|=|n-(±6)|
因为QG=QP,
82+(n-2)2=[n-(±6)]2,
解得n=-4,或n=2,
∴Q(-4,0)或Q(2,0).
点评 本题是二次函数的综合题型,其中涉及到的知识点有待定系数法确定二次函数的解析式.在求有关动点问题时要注意分析题意分情况讨论结果.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
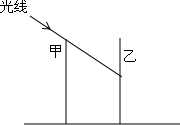 如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.
如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.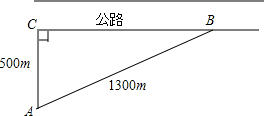 我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?
我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?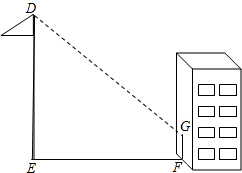 李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.
李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高. 如图,在△ABC中,AB>AC,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F,交AB、AC于E、G.
如图,在△ABC中,AB>AC,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F,交AB、AC于E、G.