题目内容
3.计算:(1)(-2)3-($\frac{1}{3}$)-1+($\sqrt{3}$-1)0+(-$\frac{2}{3}$)2017×(1.5)2016
(2)(2a+1)(2a-1)-(a+2)2-3a(a+1)
(3)($\frac{1}{a}$-1)÷$\frac{{a}^{2}-1}{{a}^{2}+a}$.
分析 (1)原式利用零指数幂、负整数指数幂法则,乘方的意义,以及幂的乘方与积的乘方运算法则计算即可得到结果;
(2)原式利用平方差公式,完全平方公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(3)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=-8-3+1+(-$\frac{2}{3}$×1.5)2016×(-$\frac{2}{3}$)=-10$\frac{2}{3}$;
(2)原式=4a2-1-a2-4a-4-3a2-3a=-7a-5;
(3)原式=-$\frac{a-1}{a}$•$\frac{a(a+1)}{(a+1)(a-1)}$=-1.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.已知P(a,3)和Q(4,b)关于x轴对称,则(a+b)2016的值为( )
| A. | 1 | B. | -1 | C. | 72016 | D. | -72016 |
12.要使分式$\frac{1}{x}$有意义,x的取值范围满足( )
| A. | x≠0 | B. | x=0 | C. | x>0 | D. | x<0 |
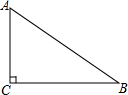 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.
如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等. 某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.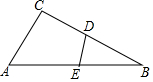 如图,在△ABC中,点D是BC边上的动点(不与点B、C重合),点E是AB边上的动点(不与点A、B重合),则当满足条件∠A=∠BDE(答案不唯一)时,△ABC与△DEB相似(写出一个即可).
如图,在△ABC中,点D是BC边上的动点(不与点B、C重合),点E是AB边上的动点(不与点A、B重合),则当满足条件∠A=∠BDE(答案不唯一)时,△ABC与△DEB相似(写出一个即可).