题目内容
14．
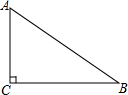如图，已知△ABC，∠C=90°，AC＜BC，D为BC上一点，且到A、B两点的距离相等．（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；
（2）连结AD，若∠B=32°，求∠CAD的度数．
分析 （1）作线段AB的垂直平分线，交BC于一点，这点就是D点位置；
（2）根据直角三角形两锐角互余可得∠BAC的度数，再根据等边对等角可得∠DAB的度数，进而可得答案．
解答 
解：（1）如图所示：点D即为所求；
（2）∵△ABC，∠C=90°，∠B=32°，
∴∠BAC=58°，
∵AD=BD，
∴∠B=∠DAB=32°，
∴∠CAD=58°-32°=26°．
点评 此题主要考查了基本作图，以及线段垂直平分线的做法，关键是掌握直角三角形两锐角互余，到线段两端点的距离相等的点在线段的垂直平分线上．
练习册系列答案
相关题目
2．在数轴上，点A表示的数是-2，那么数轴上到A点的距离是3的点表示的有理数是（ ）
| A． | 1 | B． | -5 | C． | 1 或-5 | D． | -1或5 |
9．两地的实际距离是2000m，在地图上量得这两地的距离为2cm，这幅地图的比例尺是（ ）
| A． | 1：1000000 | B． | 1：100000 | C． | 1：2000 | D． | 1：1000 |
19．若一个圆锥的底面半径为2，母线长为6，則该圆锥侧面展开图的圆心角是（ ）
| A． | 90° | B． | 100° | C． | 60° | D． | 120° |
6．在线段AB上取一点C，使AC=$\frac{1}{3}$AB，再在AB的延长线上取一点D，使DB=$\frac{1}{4}$AD，则BC是AD的（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |