题目内容
1.A(-2,y1)、B(1,y2)、C(3,y3)是抛物线y=2x2+m(m为常数)上的三个点,则y1、y2、y3的大小关系是y2<y1<y3.分析 把三点坐标代入可分别求得y1、y2、y3的值,再进行比较即可.
解答 解:
∵A(-2,y1)、B(1,y2)、C(3,y3)是抛物线y=2x2+m(m为常数)上的三个点,
∴y1=2×(-2)2+m=8+m,y2=2×12+m=2+m,y3=2×32+m=18+m,
∵m为常数,
∴2+m<8+m<18+m,
∴y2<y1<y3,
故答案为:y2<y1<y3.
点评 本题主要考查函数图象上点的坐标特征,掌握函数图象上点的坐标满足函数解析式是解题的关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
12.下列计算中,正确的是( )
| A. | $\sqrt{2}×3\sqrt{2}=4\sqrt{2}$ | B. | $\sqrt{24}$$÷\sqrt{6}$=2 | C. | $\sqrt{12}$$+\sqrt{18}$=6$\sqrt{3}$ | D. | $\sqrt{20}$-$\sqrt{5}$=4 |
10.若关于x的不等式mx-n>0的解集是x<$\frac{1}{3}$,则关于x的不等式(m+n)x>n-m的解集是( )
| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<$\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
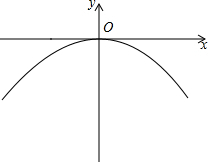 有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.
有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.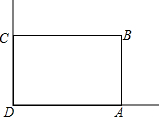 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm、花园面积为Sm2.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm、花园面积为Sm2.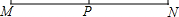 如图,已知线段MN═6cm,点P是MN的中点.分别以M、N为圆心,r1cm,r2cm为半径画圆.若点P在⊙M内,又在⊙N外.则r1的范围是r1>3,r2的范围是0<r2<3.
如图,已知线段MN═6cm,点P是MN的中点.分别以M、N为圆心,r1cm,r2cm为半径画圆.若点P在⊙M内,又在⊙N外.则r1的范围是r1>3,r2的范围是0<r2<3.