题目内容
10.若关于x的不等式mx-n>0的解集是x<$\frac{1}{3}$,则关于x的不等式(m+n)x>n-m的解集是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<$\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
分析 先解关于x的不等式mx-n>0,得出解集,再根据不等式的解集是x<$\frac{1}{3}$,从而得出m与n的关系,然后解不等式(m+n)x>n-m即可.
解答 解:∵关于x的不等式mx-n>0的解集是x<$\frac{1}{3}$,
∴m<0,$\frac{n}{m}$=$\frac{1}{3}$,
解得m=3n,
∴n<0,
∴解关于x的不等式(m+n)x>n-m得,x<$\frac{n-m}{m+n}$,
∴x<$\frac{n-3n}{3n+n}$=-$\frac{1}{2}$,
故选:A.
点评 本题考查了不等式的解集以及不等式的性质,要熟练掌握不等式的性质3.

练习册系列答案
相关题目
18.将函数y=-2x的图象向下平移3个单位,所得图象对应的函数关系式为( )
| A. | y=-2(x+3) | B. | y=-2(x-3) | C. | y=-2x+3 | D. | y=-2x-3 |
5.已知一组数据3、a、4、5、9的众数是4,则这组数据的平均数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
2.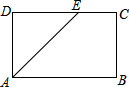 如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )
如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )
 如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )
如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
19. 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则每分出水( )
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则每分出水( )
 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则每分出水( )
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则每分出水( )| A. | $\frac{15}{4}$升 | B. | 4升 | C. | 5升 | D. | $\frac{25}{4}$升 |
 已知:如图,△ABC中,AB=AC,CE⊥AE于E,CE=$\frac{1}{2}$BC,E在△ABC外,求证:∠ACE=∠B.
已知:如图,△ABC中,AB=AC,CE⊥AE于E,CE=$\frac{1}{2}$BC,E在△ABC外,求证:∠ACE=∠B.