题目内容

4．某种商品的进价为30元/件，在某段时间内若以每件x元出售，可卖出（200-x）件．问：应如何定价才能使利润最大？

分析 本题是营销问题，基本等量关系：利润=每件利润×销售量，每件利润=每件售价-每件进价．再根据所列二次函数求最大值．

解答 解：依题意得：
y=（x-30）（200-x）
整理得：y=-x2+230x-6000=-（x-115）2+7225．
∵-1＜0，
∴当x=115时，二次函数有最大值7225，
∴定价是115元时，利润最大．

点评 本题考查了把实际问题转化为二次函数，再利用二次函数的性质进行实际应用．此题为数学建模题，借助二次函数解决实际问题．

练习册系列答案
相关题目
2．求下列各数的值，并找规律．
$\root{3}{{2}^{3}}$=2，$\root{3}{（-2）^{3}}$=-2，$\root{3}{（-3）^{3}}$=-3，$\root{3}{{4}^{3}}$=4，$\root{3}{{0}^{3}}$=0．
结论：对于任何数a都有$\root{3}{{a}^{3}}$=a．
15．已知多边形一个内角的外角与其他各内角和为600°，则该多边形的边数为（　　）
A．5B．6
C．5或6D．不存在这样的多边形
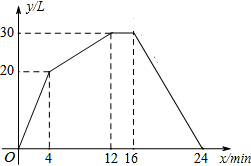12．一蓄水池每单位时间内的进、出水量都是一定的，设某时刻开始只进水，不出水，随后既进水又出水，然后既不进水，也不出水，最后只出水不进水，直到将水池中的水放尽，蓄水池中的水量y（L）与时间x（min）之间的关系如图．根据图象解决下列问题：
（1）进水管每分钟进水多少升？
（2）出水管每分钟出水多少升？
（3）蓄水池有多长时间既不进水也不出水？
19．计算：
（1）（$\frac{6}{5}$）3÷（$\frac{5}{6}$）-3+（-$\frac{3}{2}$）2÷（$\frac{2}{3}$）-3-（$\frac{1}{3}$-3）0+3-1；
（2）[（x+y）2n]4÷（-x-y）2n+1．
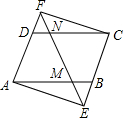9．如图，在?ABCD中，E，F分别是CB，AD延长线上的点，连接AE，CF，若四边形AECF是平行四边形，且对角线EF分别交?ABCD的两边AB，CD于点M，N，求证：EM=FN．
16．已知正比例函数的图象过点（3，-2）和（n，6）．
（1）求正比例函数的表达式；
（2）求n的值．
13．菱形的两条对角线长为6cm和8cm，那么这个菱形的周长为（　　）
A．40cmB．20cmC．10cmD．5cm
14．下面函数中，是正比例函数的是（　　）
A．y=6xB．y=$\frac{-6}{x}$C．y=x2+6xD．y=3x-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网