题目内容
15．已知多边形一个内角的外角与其他各内角和为600°，则该多边形的边数为（ ）| A． | 5 | B． | 6 | ||
| C． | 5或6 | D． | 不存在这样的多边形 |
分析 根据n边形的内角和定理可知：n边形内角和为（n-2）×180°．设这个外角度数为x度，利用方程即可求出答案．
解答 解：设这个外角度数为x，根据题意，得
（n-2）×180°+x=600°，
解得：x=600°-180°n+360°=960°-180°n，
由于0＜x＜180°，即0＜960°-180°n＜180°，
解得4$\frac{1}{3}$＜n＜5$\frac{1}{3}$，
所以n=5．
故这个多边形的边数为5．
故选A．
点评 主要考查了多边形的内角和定理．n边形的内角和为：180°•（n-2）．
练习册系列答案
发散思维新课堂系列答案
相关题目
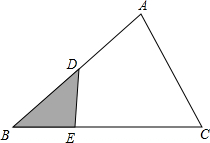已知△ABC的面积是80cm2，DE把△ABC分为两块，已知AD=BD，CE=4BE，求△BDE的面积．
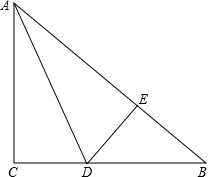如图所示，已知在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB于点E，△DEB的周长为8cm，则AB=8cm．
图中两个三角形全等吗？请说明理由．