题目内容
19.计算:(1)($\frac{6}{5}$)3÷($\frac{5}{6}$)-3+(-$\frac{3}{2}$)2÷($\frac{2}{3}$)-3-($\frac{1}{3}$-3)0+3-1;
(2)[(x+y)2n]4÷(-x-y)2n+1.
分析 (1)首先利用负整数指数幂的性质以及零指数幂的性质化简,进而求出即可;
(2)利用幂的乘方运算以及同底数幂的除法运算法则求出即可.
解答 解:(1)($\frac{6}{5}$)3÷($\frac{5}{6}$)-3+(-$\frac{3}{2}$)2÷($\frac{2}{3}$)-3-($\frac{1}{3}$-3)0+3-1
=($\frac{6}{5}$)3÷$\frac{1}{(\frac{5}{6})^{3}}$+(-$\frac{3}{2}$)2÷$\frac{1}{(\frac{2}{3})^{3}}$-1+$\frac{1}{3}$
=($\frac{6}{5}$)3×($\frac{5}{6}$)3+(-$\frac{3}{2}$)2×($\frac{2}{3}$)3-1+$\frac{1}{3}$
=1+$\frac{2}{3}$-1+$\frac{1}{3}$
=1;
(2)[(x+y)2n]4÷(-x-y)2n+1
=(x+y)8n÷(-x-y)2n+1
=-(x+y)6n-1.
点评 此题主要考查了负整数指数幂的性质以及零指数幂的性质和同底数幂的除法运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
 图中两个三角形全等吗?请说明理由.
图中两个三角形全等吗?请说明理由.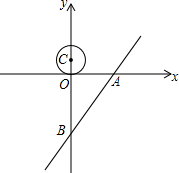 如图所示,直线l的解析式是y=$\frac{4}{3}$x-4,并且与x轴、y轴分别交于A、B点.一个半径为1.5的⊙C,点C坐标为(0,1.5),圆心C以第秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,⊙C运动的时间为( )秒.
如图所示,直线l的解析式是y=$\frac{4}{3}$x-4,并且与x轴、y轴分别交于A、B点.一个半径为1.5的⊙C,点C坐标为(0,1.5),圆心C以第秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,⊙C运动的时间为( )秒.