题目内容
4.方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x+y=2①}\\{2x-y=1②}\end{array}\right.$,
①+②得:3x=3,即x=1,
把x=1代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
故选D.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
12.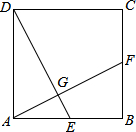 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
9. 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
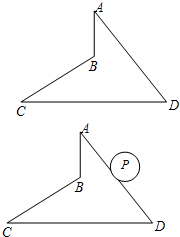 如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10. 在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.
在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1. 如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.
如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.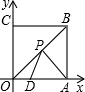 如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$.
如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$.