题目内容
15.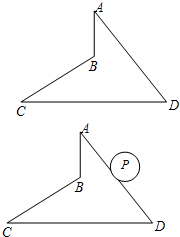 如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.(1)求AB、BC的长;
(2)已知,半径为1的⊙P在四边形ABCD的外面沿各边滚动(无滑动)一周,求⊙P在整个滚动过程中所覆盖部分图形的面积.
分析 (1)延长AB交CD于E,先求出∠AED=90°,得出∠CEB=90°,运用三角函数得出DE、AE,求出CE,即可得出BC、BE、AB;
(2)根据题意得出:∠1=120°,∠2=∠3=150°,∠4=∠5=60°,HF=HG=2,运用三角函数得出BF=BG=$\frac{2\sqrt{3}}{3}$,⊙P在整个滚动过程中所覆盖部分图形的面积=4个矩形的面积+2个三角形的面积+3个扇形的面积,即可得出结果.
解答 解:(1)延长AB交CD于E,如图1所示: 则∠AED=180°-∠A-∠D=180°-30°-60°=90°,
则∠AED=180°-∠A-∠D=180°-30°-60°=90°,
∴∠CEB=90°,
∴DE=$\frac{1}{2}$AD=4,AE=AD•sin60°=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∴CE=CD-DE=6,
∴BC=$\frac{CE}{cos30°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$,
∴BE=$\frac{1}{2}$BC=2$\sqrt{3}$,
∴AB=AE-BE=$2\sqrt{3}$;
(2)半径为1的⊙P在四边形ABCD的外面沿各边滚动(无滑动)一周,如图2所示:
根据题意得:∠1=120°,∠2=∠3=150°,∠4=∠5=60°,HF=HG=2,
∴BF=BG=$\frac{HF}{tan60°}$=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$,
∴CF=4$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$,AG=2$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴⊙P在整个滚动过程中所覆盖部分图形的面积
=8×2+10×2+$\frac{10\sqrt{3}}{3}$×2+$\frac{4\sqrt{3}}{3}$×2+$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×2×2+$\frac{120+150+150}{360}π×{2}^{2}$
=36+$\frac{32\sqrt{3}}{3}$$+\frac{14π}{3}$.
点评 本题是圆的综合题目,考查了直角三角形的判定、三角函数、扇形面积、矩形面积以及三角形面积的计算等知识;本题有一定难度,综合性强,特别是(2)中,得出⊙P在整个滚动过程中所覆盖部分图形的面积=4个矩形的面积+2个三角形的面积+3个扇形的面积是解决问题的关键.

 甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )
甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )| A. | 甲的速度为60千米/小时 | B. | 乙从A地到B地用了3小时 | ||
| C. | 甲比乙晚出发0.5小时 | D. | 甲到达B地时,乙离A地80千米 |
| A. | a×a=a2n | B. | -(-a)=a | C. | a×a×a=a | D. | a•(-a)=-a |
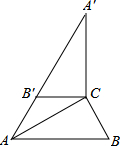 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )| A. | 6 | B. | $4\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 3 |
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
 如图,△ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:CF=2AF.
如图,△ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:CF=2AF. 汽车油箱中原有汽油若干,如果不再加油,那么油箱中的剩油量y(单位:L)与行驶路程x(单位:km)的寒素关系如图.
汽车油箱中原有汽油若干,如果不再加油,那么油箱中的剩油量y(单位:L)与行驶路程x(单位:km)的寒素关系如图.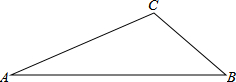 如图,已知△ABC
如图,已知△ABC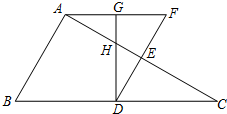 如图,△ABC中,BC=2AB,点D、E分别是BC、AC的中点,过点A作AF∥BC交线段DE的延长线于点F,取AF的中点G,联结DG,GD与AE交于点H.
如图,△ABC中,BC=2AB,点D、E分别是BC、AC的中点,过点A作AF∥BC交线段DE的延长线于点F,取AF的中点G,联结DG,GD与AE交于点H.