题目内容
9. 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
分析 由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,即可证得△DEF∽△BAF,然后由相似三角形面积比等于相似比的平方,即可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△DEF∽△BAF,
∴$\frac{{S}_{△DEF}}{S△ABF}$=${(\frac{DE}{AB})}^{2}$,
∵DE:EC=2:3,
∴DE:CD=DE:AB=2:5,
∴S△DEF:S△ABF=4:25.
故选A.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.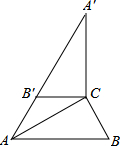 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )| A. | 6 | B. | $4\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 3 |
4.方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
14.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{9}$ |
1.已知$\sqrt{a}$是二次根式,则a的值可以是( )
| A. | -2 | B. | -1 | C. | 2 | D. | -7 |
18.下列四个点中,位于第三象限的是( )
| A. | (2015,2014) | B. | (2014,-2015) | C. | (-2014,-2015) | D. | (-2015,2014) |
19.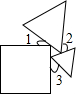 一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
 一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )| A. | 180° | B. | 100° | C. | 90° | D. | 80° |