题目内容
1.把一个自然数所有数位上的数字先平方再求和得到一个新数,叫做第一次运算,再把所得新数所有数位上的数字先平方再求和又将得到一个新数,叫做第二次运算,…如此重复下去,若最终结果为1,我们把具有这种特征的自然数称为“快乐数”.例如:32→32+22=13→12+32=10→12+02=1,
70→72+02=49→42+92=97→92+72=130→12+32+02=10→12+02=1
所以32和70都是“快乐数”.
(1)最小的两位“快乐数”是10;
(2)证明19是“快乐数”;
(3)若一个三位“快乐数”经过两次运算后结果为1,把这个三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2,求出这个“快乐数”.
分析 (1)根据快乐数的定义即刻得到结论;
(2)由19经过两次运算后结果为1,于是得到结论;
(3)设三位“快乐数”为abc,由题意,经过两次运算后结果为1,所以第一次运算后结果一定是10或者100,所以a2+b2+c2=10或100即可得出结论;
解答 解:(1)最小的两位“快乐数”是10,
故答案为:10;
(2)∵19→12+92=82→82+22=68→62+82=100→12+02+02=1,
∴19是快乐数;
(3)设三位“快乐数”为abc,由题意,经过两次运算后结果为1,所以第一次运算后结果一定是10或者100,所以a2+b2+c2=10或100,
∵a,b,c为整数,且a≠0,∴a2+b2+c2=10 时,
∴12+32+02=10,
?当a=1时,b=3或0,c=0或3,三位“快乐数”为130,103,
当a=3时,b=1或0,c=0或1,三位“快乐数”为310,301,
同理当a2+b2+c2=10时,因为62+82+02=100,所以三位“快乐数”有680,608,806,860,
综上一共有130,103,310,301,680,608,806,860八个.又因为三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2,所以只有310和860满足已知条件.
点评 本题考查了因式分解的应用,读懂题意弄清“快乐数”的判定是解题的关键.

练习册系列答案
相关题目
16.若“?”是某种新规定的运算符号,设a?b=3a+2b,则[(x+y)?(x-y)]?3x化简为( )
| A. | 0 | B. | 21x+3y | C. | 5x | D. | 9x+6y |
 如图,在△ABC中,D是AB中点,联结CD.
如图,在△ABC中,D是AB中点,联结CD.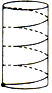 为筹备元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图,已知圆筒高108cm,其平行底面的截面周长为36cm,如果在表面缠绕4圈,需要油纸的长度为180cm.
为筹备元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图,已知圆筒高108cm,其平行底面的截面周长为36cm,如果在表面缠绕4圈,需要油纸的长度为180cm.