题目内容
10. 如图,在△ABC中,D是AB中点,联结CD.
如图,在△ABC中,D是AB中点,联结CD.(1)若AB=10且∠ACD=∠B,求AC的长.
(2)过D点作BC的平行线交AC于点E,设$\overrightarrow{DE}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,请用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示$\overrightarrow{AC}$和$\overrightarrow{AB}$(直接写出结果)
分析 (1)求出AD=$\frac{1}{2}$AB=5,证明△ACD∽△ABC,得出$\frac{AC}{AB}=\frac{AD}{AC}$,即可得出结果;
(2)由平行线的性质得出AE=EC,由向量的定义容易得出结果.
解答 解:(1)∵D是AB中点,
∴AD=$\frac{1}{2}$AB=5,
∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AB•AD=10×5=50,
∴AC=$\sqrt{50}$=5$\sqrt{2}$;
(2)如图所示:∵DE∥BC,D是AB的中点,
∴AD=DB,AE=EC,
∵$\overrightarrow{DE}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,
∴$\overrightarrow{AE}=\overrightarrow{EC}$=$\overrightarrow{DC}-\overrightarrow{DE}$=$\overrightarrow{b}-\overrightarrow{a}$,
∴$\overrightarrow{AC}=-2\overrightarrow{a}+2\overrightarrow{b}$,
∵$\overrightarrow{AD}=\overrightarrow{AE}-\overrightarrow{DE}$=$\overrightarrow{b}-\overrightarrow{a}-\overrightarrow{a}$=$\overrightarrow{b}-2\overrightarrow{a}$,
∴$\overrightarrow{AB}=-4\overrightarrow{a}+2\overrightarrow{b}$.
点评 本题考查了相似三角形的判定与性质、平面向量、平行线的性质;熟练掌握相似三角形的判定与性质是解决问题的关键.

 某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩成绩统计表
| 成绩 | 划记 | 频数 | 频率 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 |   | c | d |
| 合计 |
请根据以上信息,解答下列问题:
(1)表中的a=18;b=0.5;c=3;d=0.05.
(2)请根据频数分布表,画出相应的频数分布直方图.

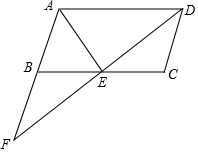 如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.
如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.