��Ŀ����
1�� ��ͼ��ֱ��l1��l2��ֱ��l��l1��l2�ֱ���A��B���㣬��M��N�ֱ���l1��l2�ϣ���M��N��P����l��ͬ�ࣨ��P����l1��l2�ϣ�������PAM=������PBN=�£�
��ͼ��ֱ��l1��l2��ֱ��l��l1��l2�ֱ���A��B���㣬��M��N�ֱ���l1��l2�ϣ���M��N��P����l��ͬ�ࣨ��P����l1��l2�ϣ�������PAM=������PBN=�£���1������P��l1��l2֮��ʱ��
�����APB�Ĵ�С���ú������µĴ���ʽ��ʾ����
������APM��ƽ�������PBN��ƽ���߽��ڵ�P1����P1AM��ƽ�������P1BN��ƽ���߽��ڵ�P2��������Pn-1AM��ƽ�������Pn-1BN��ƽ���߽��ڵ�Pn�����AP1B=$\frac{��+��}{2}$����APnB=$\frac{��+��}{{2}^{n}}$�����ú������µĴ���ʽ��ʾ������nΪ��������
��2������P����l1��l2֮��ʱ��
����PAM��ƽ�������PBN��ƽ���߽��ڵ�P����P1AM��ƽ�������P1BN��ƽ���߽��ڵ�P2��������Pn-1AM��ƽ�������Pn-1BN��ƽ���߽��ڵ�Pn����ֱ��д����APnB�Ĵ�С�����ú������µĴ���ʽ��ʾ������nΪ��������
���� ��1������P��PQ��l1��AB��Q�����APQ=��MAP=�����ɡ�APQ=��MAP=���٣���QPB=��PBN=�¢ڣ���+�ڼ��ɽ�����⣮
��2�����ã�1���Ľ��ۼ��ɽ�����⣮
��3������������д�����ۼ��ɣ�
���  �⣺��1������P��PQ��l1��AB��Q�����APQ=��MAP=�� ��
�⣺��1������P��PQ��l1��AB��Q�����APQ=��MAP=�� ��
��l1��l2��
��PQ��l2��
���QPB=��PBN=�� �ڣ�
��+�ڵá�APQ+��BPQ=��MAP+��PBN��
���APB=��+�£�
��2���ɣ�1����֪��P1=$\frac{1}{2}$����+�£�����p2=$\frac{1}{4}$����+�£�����p3=$\frac{1}{8}$����+�£���
���APnB=$\frac{��+��}{{2}^{n}}$��
�ʴ𰸷ֱ�Ϊ$\frac{��+��}{2}$��$\frac{��+��}{{2}^{n}}$��
��3����P��l1�Ϸ�ʱ���£�������APnB=$\frac{��-��}{{2}^{n}}$��
����P��l2�·�ʱ�������£���ApnB=$\frac{��-��}{{2}^{n}}$��
���� ���⿼��ƽ���ߵ����ʣ��ǵĺͲ���֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ������һ�㣬̽�����ɣ����ù��ɽ�����⣬�����п��������ͣ�

��ϰ��ϵ�д�
�����Ŀ
17������������ȷ���ǣ�������
| A�� | -a•a3=a3 | B�� | -��a2��2=a4 | C�� | x-$\frac{1}{3}$x=$\frac{2}{3}$ | D�� | ��$\sqrt{3}$-2����$\sqrt{3}$+2��=-1 |
16�� ��AD��BE���ҡ�ACB=90�㣬��CBE=30�㣬���CAD�Ķ���Ϊ��������
��AD��BE���ҡ�ACB=90�㣬��CBE=30�㣬���CAD�Ķ���Ϊ��������
 ��AD��BE���ҡ�ACB=90�㣬��CBE=30�㣬���CAD�Ķ���Ϊ��������
��AD��BE���ҡ�ACB=90�㣬��CBE=30�㣬���CAD�Ķ���Ϊ��������| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
13�����и�ʽ�У�������Ϊm2-4n2���ǣ�������
| A�� | ��-m-2n�� 2n | B�� | ��m-2n����2n-m�� | C�� | ��m-2n����-m-2n�� | D�� | ��2n-m����-m-2n�� |
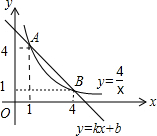 ��ͼ��һ�κ���y=kx+b��k��bΪ��������k��0���ͷ���������y=$\frac{4}{x}$��x��0����ͼ����A��B���㣬���ú���ͼ��ֱ��д������ʽ$\frac{4}{x}$��kx+b�Ľ⼯��1��x��4��
��ͼ��һ�κ���y=kx+b��k��bΪ��������k��0���ͷ���������y=$\frac{4}{x}$��x��0����ͼ����A��B���㣬���ú���ͼ��ֱ��д������ʽ$\frac{4}{x}$��kx+b�Ľ⼯��1��x��4��

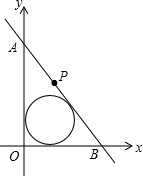 �Ķ����⣺�����������a��b����a��0��b��0��������IJ���ʽ��$\frac{a+b}{2}$$��\sqrt{ab}$�����ҽ���a=bʱȡ���Ⱥ����ǰ�$\frac{a+b}{2}$��������a��b������ƽ��������$\sqrt{ab}$��������a��b�ļ���ƽ������������������ʽ�ɱ���Ϊ����������������ƽ������С�ڣ������ڻ���ڣ����ǵļ���ƽ������������ѧ���й㷺��Ӧ�ã��ǽ����ֵ������������ߣ�
�Ķ����⣺�����������a��b����a��0��b��0��������IJ���ʽ��$\frac{a+b}{2}$$��\sqrt{ab}$�����ҽ���a=bʱȡ���Ⱥ����ǰ�$\frac{a+b}{2}$��������a��b������ƽ��������$\sqrt{ab}$��������a��b�ļ���ƽ������������������ʽ�ɱ���Ϊ����������������ƽ������С�ڣ������ڻ���ڣ����ǵļ���ƽ������������ѧ���й㷺��Ӧ�ã��ǽ����ֵ������������ߣ�