题目内容
13.如图1,点A,B,C在⊙O上,连结OC,OB,(1)求证:∠BAC=∠B+∠C;
(2)若点A在如图2的位置,以上结论仍成立吗?请说明理由.

分析 (1)连接OA,由OA=OB,OA=OC,利用等边对等角即可.
(2)同(1),连接OA,由OA=OB,OA=OC,利用等边对等角即可证得结论成立.
解答  (1)证明:连接OA,
(1)证明:连接OA,
∵OA=OB,OA=OC,
∴∠BAO=∠B,∠CAO=∠C,
∴∠BAC=∠BAO+∠CAO=∠B+∠C.
(2)成立.
理由:连接OA,
∵OA=OB,OA=OC,
∴∠BAO=∠B,∠CAO=∠C,
∴∠BAC=∠BAO+∠CAO=∠B+∠C;
点评 此题考查了圆周角的性质、等腰三角形的性质.此题比较简单,解题的关键是注意掌握数形结合思想的应用,注意准确作出辅助线.

练习册系列答案
相关题目
3. 实数a、b在数轴上的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$=( )
实数a、b在数轴上的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$=( )
 实数a、b在数轴上的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$=( )
实数a、b在数轴上的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$=( )| A. | 2a | B. | 2b | C. | -2a | D. | -2b |
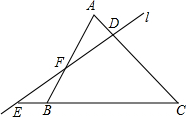 如图,已知直线l截△ABC三边所在的直线分别于E、F、D三点,且AD=BE,求证:EF:FD=CA:CB.
如图,已知直线l截△ABC三边所在的直线分别于E、F、D三点,且AD=BE,求证:EF:FD=CA:CB.