题目内容
12.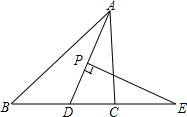 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E①若∠B=35°,∠ACB=85°,求∠E的度数.
②猜想∠E与∠B、∠ACB的数量关系.
分析 ①中,首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;
②中,根据第(1)小题的思路即可推导这些角之间的关系.
解答 解:①∵∠B=35°,∠ACB=85°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠DAC=30°,
∴∠ADC=65°,
∴∠E=25°;
②∠E=$\frac{1}{2}$(∠ACB-∠B).
设∠B=n°,∠ACB=m°,
∵AD平分∠BAC,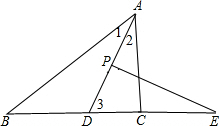
∴∠1=∠2=$\frac{1}{2}$∠BAC,
∵∠B+∠ACB+∠BAC=180°,
∵∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠BAD=$\frac{1}{2}$(180-n-m)°,
∴∠3=∠B+∠1=n°+$\frac{1}{2}$(180-n-m)°=90°+$\frac{1}{2}$n°-$\frac{1}{2}$m°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+$\frac{1}{2}$n°-$\frac{1}{2}$m°)=$\frac{1}{2}$(m-n)°=$\frac{1}{2}$(∠ACB-∠B).
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
1.下列各组数中,互为相反数的是( )
| A. | |-$\frac{1}{3}$|和-$\frac{1}{3}$ | B. | |-$\frac{1}{3}$|和-3 | C. | |-$\frac{1}{3}$|和$\frac{1}{3}$ | D. | |-$\frac{1}{3}$|和3 |
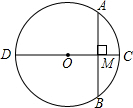 如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.
如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.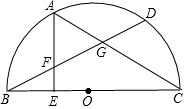 已知:如图,BC是半⊙O的直径,点D在半⊙O,上点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.
已知:如图,BC是半⊙O的直径,点D在半⊙O,上点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G. 已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )
已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )



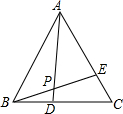 如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数.
如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数. 如图,点P是∠BOA的平分线OC上一点,PE⊥OB于点E.已知PE=3,则点P到OA的距离是( )
如图,点P是∠BOA的平分线OC上一点,PE⊥OB于点E.已知PE=3,则点P到OA的距离是( )