题目内容
12.若$\frac{2x+y}{3}$=$\frac{x+3y}{5}$=1,将原方程组化为$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的形式为$\left\{\begin{array}{l}{2x+y=3}\\{x+3y=5}\end{array}\right.$.分析 把原式化为:$\frac{2x+y}{3}$=1和$\frac{x+3y}{5}$=1,然后进行整理,得到二元一次方程组.
解答 解:原式可化为:$\frac{2x+y}{3}$=1和$\frac{x+3y}{5}$=1,
整理得,$\left\{\begin{array}{l}{2x+y=3}\\{x+3y=5}\end{array}\right.$.
点评 本题考查的是二元一次方程组的定义,把连等式化为两式相等的形式,然后根据等式的性质整理,可以化为二元一次方程组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.
如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.
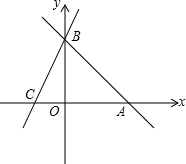 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.