题目内容
17.我市某中学矩形了“关爱留守儿童”的“义捐义卖”活动,并把所筹集到的部分善款购买了A,B两种学习用品捐赠给小黑和他所在的学校.已知A学习用品比B学习用品每件便宜10元,且购买4件A学习用品和6件B学习用品共需花费260元.(1)求A、B两种学习用品每件多少元?
(2)若购买1000件这两种用品花费资金不超过28000元,求最多能购买B种用品多少件?
分析 (1)设A种学习用品每件x元,B种学习用品每件y元,由总价=A、B两种学习用品的价格之和建立方程组求出其解即可;
(2)设购买B种学习用品a件,则购买A种学习用品(1000-a)件,根据两种用品花费资金不超过28000元建立不等式,求出其解即可.
解答 解:(1)A种学习用品每件x元,B种学习用品每件y元,由题意,得
$\left\{\begin{array}{l}{y-x=10}\\{4x+6y=260}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$.
答:A种学习用品每件20元,B种学习用品每件30元;
(2)设购买B种学习用品a件,则购买A种学习用品(1000-a)件,由题意,得
30a+20(1000-a)≤28000,
解得:a≤800.
∴a最大值为800.
答:最多能购买B种用品800件.
点评 本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,列一元一次不等式解实际问题的运用,解答时根据题意的等量关系及不相等关系建立方程及不等式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若3a=2,3b=6,3c=12,a,b,c的关系不正确的是( )
| A. | b=a+1 | B. | c=a+b+1 | C. | 2b=c+1 | D. | c=2a+1 |
15.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
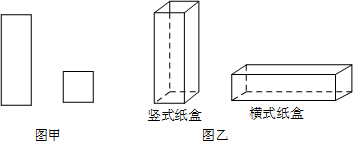
(1)根据题意,完成以下表格:
(2)按两种纸盒的生产个数来分,有哪几种生产方案?
(3)如果做一个竖式纸盒的费用为2元,做一个横式纸盒的费用为1元,如何安排设计方案,使得生产费用最少?

(1)根据题意,完成以下表格:
(2)按两种纸盒的生产个数来分,有哪几种生产方案?
(3)如果做一个竖式纸盒的费用为2元,做一个横式纸盒的费用为1元,如何安排设计方案,使得生产费用最少?
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | 100-x | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |
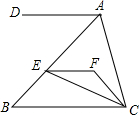 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=105°,∠ACF=25°.求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=105°,∠ACF=25°.求∠FEC的度数.