题目内容
4．先化简，再求值：$\frac{x+1}{x-1}$-$\frac{{x}^{2}-2x}{{x}^{2}-1}$÷$\frac{{x}^{2}-x-2}{{x}^{2}+2x+1}$，其中x=2015．分析 原式第二项利用除法法则变形，约分后利用同分母分式的减法法则计算得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{x+1}{x-1}$-$\frac{x（x-2）}{（x+1）（x-1）}$•$\frac{（x+1）^{2}}{（x-2）（x+1）}$=$\frac{x+1}{x-1}$-$\frac{x}{x-1}$=$\frac{1}{x-1}$，
当x=2015时，原式=$\frac{1}{2014}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
15．边长为4的等边三角形的中位线长为（ ）
| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A，点A在第一象限内且满足b=2t，设OA与x轴正方向的夹角为α，求tanα的取值范围．
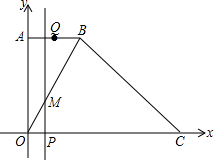如图，在平面直角坐标系中，已知A（0，4），B（2，4），点C在x轴的正半轴上，且∠BCO=45°，连接OB．动点Q以每秒1个单位长度的速度，从点B沿折线B-A-O向点O运动．同时动点P以相同的速度，从点O沿线段OC向点C运动．过点P作直线PM⊥OC，与折线O-B-C相交于点M．当其中一点到达终点时，另一点也随之停止运动．设点P运动时间为t（秒）．
已知，如图所示，在Rt△ABC中，∠C=90°，