题目内容
7.如图,四边形ABCD是正方形,点G是BC上一点,DE⊥AG于点E,BF∥DE且交AG于点F.(1)如图1,求证:AE=BF;
(2)如图2,当∠BAG=30°,且AB=2时,求EF-FG的值.
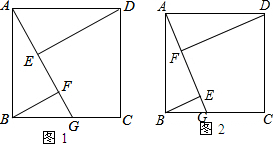
分析 (1)首先根据角角之间的等量代换得到∠ABF=∠DAE,结合AB=AD,∠AED=∠BFA,利用AAS证明△ABF≌△DAE,即可得到AE=BF;
(2)首先求出BF和AE的长度,然后在Rt△BFG中求出BG=2FG,利用勾股定理得到BG2=FG2+BF2,进而求出FG的长,于是可得EF-FG的值.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠DAE=∠BAD=90°,
又∵DE⊥AG,BF∥DE,
∴∠AED=∠BFA=90°,
∵∠BAF+∠ABF=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABF=∠DAE}\\{∠AED=∠BFA}\end{array}\right.$,
∴△ABF≌△DAE(AAS),
∴AE=BF;
(2)解:∵∠BAG=30°,AB=2,∠BEA=90°,
∴BF=$\frac{1}{2}$AB=1,AF=$\sqrt{A{B}^{2}-B{F}^{2}}=\sqrt{3}$,
∴EF=AF-AE=AF-BF=$\sqrt{3}$-1,
∵BF⊥AG,∠ABG=90°,∠BAG=30°,
∴∠FBC=30°,
∴BG=2FG,
由BG2=FG2+BF2,
∴4FG2=FG2+1,
∴FG=$\frac{\sqrt{3}}{3}$,
∴EF-FG=$\sqrt{3}$-1-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$-1.
点评 本题主要考查了正方形的性质、全等三角形的判定与性质以及勾股定理等知识,解答本题的关键是根据AAS证明△ABF≌△DAE,此题难度一般.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
17.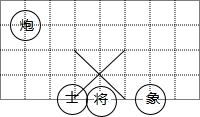 如图,若在象棋盘上建立直角坐标系,使“将”位于点(0,-1),“象”位于(2,-1),则“炮”位于点( )
如图,若在象棋盘上建立直角坐标系,使“将”位于点(0,-1),“象”位于(2,-1),则“炮”位于点( )
 如图,若在象棋盘上建立直角坐标系,使“将”位于点(0,-1),“象”位于(2,-1),则“炮”位于点( )
如图,若在象棋盘上建立直角坐标系,使“将”位于点(0,-1),“象”位于(2,-1),则“炮”位于点( )| A. | (-3,2) | B. | (-4,3) | C. | (-3,0) | D. | (1,-1) |
18.下列图形中,由∠1=∠2,能说明AB∥CD的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
15.边长为4的等边三角形的中位线长为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
 已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A,点A在第一象限内且满足b=2t,设OA与x轴正方向的夹角为α,求tanα的取值范围.
已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A,点A在第一象限内且满足b=2t,设OA与x轴正方向的夹角为α,求tanα的取值范围.