题目内容
13.已知21=2,22=4,23=8,24=16,25=32,26=64,…,那么(2+1)(22+1)(24+1)…(232+1)+1的个位数字是6.分析 原式乘以(2-1),再依次根据平方差公式进行计算,求出结果,再根据2的整数次幂的个位数字的规律,可判断最后结果的个位数字.
解答 解:原式=(2-1)(2+1)(22+1)(24+1)…(232+1)+1
=(22-1)(22+1)(24+1)…(232+1)+1
=(24-1)(24+1)…(232+1)+1
=264-1+1
=264,
∵21=2,22=4,23=8,24=16,25=32,…
∴2的整数次幂的个位数字每4个数字为一个循环组依次循环,
∵64=16×4,
∴264的个位数字与24的个位数字相同,为6,
故答案为:6.
点评 本题考查了平方差公式的应用,能灵活运用平方差公式进行计算是解此题的关键,注意:(a+b)(a-b)=a2-b2.

练习册系列答案
相关题目
5. 如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )
如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )
 如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )
如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
 如图,如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$.
如图,如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$. 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.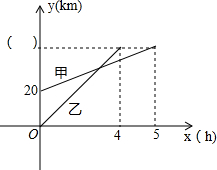 甲、乙两车分别从A,B两市相向而行,甲先行0.5小时,乙才出发,行驶4小时后到达A市,两车行驶的路程y(km)与乙车人出发后x(h)的函数关系.根据图象请回答下列问题:
甲、乙两车分别从A,B两市相向而行,甲先行0.5小时,乙才出发,行驶4小时后到达A市,两车行驶的路程y(km)与乙车人出发后x(h)的函数关系.根据图象请回答下列问题: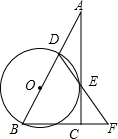 在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F,且BD=BF.
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F,且BD=BF.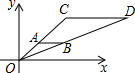 如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是(6,3).
如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是(6,3).