题目内容
18.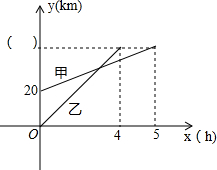 甲、乙两车分别从A,B两市相向而行,甲先行0.5小时,乙才出发,行驶4小时后到达A市,两车行驶的路程y(km)与乙车人出发后x(h)的函数关系.根据图象请回答下列问题:
甲、乙两车分别从A,B两市相向而行,甲先行0.5小时,乙才出发,行驶4小时后到达A市,两车行驶的路程y(km)与乙车人出发后x(h)的函数关系.根据图象请回答下列问题:(1)在( )中填入适当的数;
(2)乙车出发多少小时后两车相遇?
(3)乙车出发多少小时后两车相距10km?
分析 (1)先仔细观察横纵坐标轴的实际意义,根据y轴上的数据20,计算出甲的速度;因为x轴表示的是乙车人出发后的时间,所以甲车人出发的时间要在乙车时间的基础上加0.5h,这样可得出甲行驶的路程,从而确定( )内的数字;
(2)利用待定系数法确定甲乙两段图象的函数解析式,让两个函数解析式相等能求出交点即两车相遇的时间;
(3)两车相距10km要考虑到有相遇前和相遇后的两种情况,将两个函数解析式分别相减可以求解.
解答 解:(1)甲的速度:20÷0.5=40(km/h),
甲的路程:40×5.5=220(km),
在( )中填入220;
(2)设甲的函数解析式为:y=kx+b,
把(0,20)与(5,220),代入得$\left\{\begin{array}{l}{b=20}\\{5k+b=220}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=40}\\{b=20}\end{array}\right.$.
故甲的函数解析式为:y=40x+20.
设乙的函数解析式为:y=kx,把(4,220)代入得:220=4k 解得:k=55,
乙的函数解析式为:y=55x.
甲乙两车相遇:40x+20=55x,解得:x=$\frac{4}{3}$.
答:乙车出发 $\frac{4}{3}$小时后两车相遇.
(3)有两种情况:第一种甲乙相遇前:甲的路程-乙的路程:40x+20-55x=10,解得x=$\frac{2}{3}$;
第二种甲乙相遇后:乙的路程-甲的路程:55x-(40x+20)=10,解得x=2.
答 乙车出发$\frac{2}{3}$小时和2小时后两车相距10km.
点评 此题考查了一次函数的应用,弄清图形中横纵坐标的隐藏意义是关键.甲的行驶时间是易错点.

| A. | x≠3 | B. | x>$\frac{1}{2}$且x≠3 | C. | x≥2 | D. | x≥$\frac{1}{2}$且x≠3 |
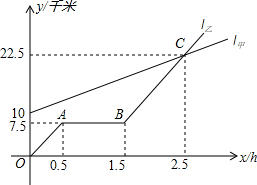 如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题:
如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题: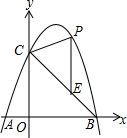 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).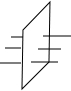 如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.
如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.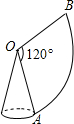 如图,有一圆心角为120°,半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是4$\sqrt{2}$ cm.
如图,有一圆心角为120°,半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是4$\sqrt{2}$ cm.