题目内容
10．已知直线y=5x+k与抛物线y=x2+3x+5交点的横坐标为1，则该直线与抛物线有几个交点？分析 首先把x=1分别代入抛物线y=x2+3x+5求得纵坐标，再代入直线y=5x+k求得k，进一步与抛物线y=x2+3x+5联立方程求得答案即可．
解答 解：把x=1分别代入抛物线y=x2+3x+5=9，
把（1，9）代入直线y=5x+k解得k=4，
由题意得
$\left\{\begin{array}{l}{y=5x+4}\\{y={x}^{2}+3x+5}\end{array}\right.$，
整理得x2-2x+1=0，
所以△=22-4×1×1=0，
故该直线与抛物线有1个交点．
点评 本题考查了二次函数的性质，一次函数的性质，以及一元二次方程根的判别式，是常见题型，要熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
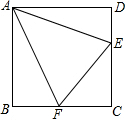已知：如图，在正方形ABCD中，AD=AB，∠D=∠ABC=∠BAD=90°，E，F分别为DC，BC边上的点，且∠EAF=45°，连接EF，求证：EF=BF+DE．
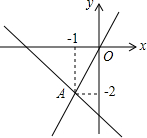如图，在平面直角坐标系中，一次函数y=k1x+b与正比例函数y=k2x的图象交于点A，则关于x的不等式k1x+b＜k2x的解集为x＞-1．
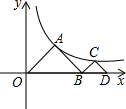如图，△AOB，△CBD是等腰直角三角形，点A、C在函数y=$\frac{4}{x}$（x＞0）的图象上，斜边OB，BD都在x轴上，则点D的横坐标是4$\sqrt{2}$．
如图：在矩形ABCD中，DE⊥AC，垂足为E，图中与△ABC相似的三角形有△ADC，△DEC，△ADE．
2．下面各整式能直接运用完全平方公式分解因式的是（ ）
| A． | x2-x+1 | B． | x2+2x-1 | C． | -2x+x2+1 | D． | 2x-x2+1 |