题目内容
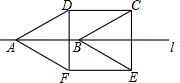
5．
如图，△ABC中，∠BAC=70°，将△ABC绕点C顺时针旋转一定角度，得到△DEC，点A的对应点为D，ED过点A，则旋转角的度数为（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |
分析 根据旋转的性质和等腰三角形的性质得到AC=CD，∠D=∠BAC=70°，然后根据三角形的内角和即可得到结论．
解答 解：∵将△ABC绕点C顺时针旋转一定角度，得到△DEC，
∴AC=CD，∠D=∠BAC=70°，
∴∠ACD=180°-∠D-∠CAD=40°，
故选C．
点评 本题考查了旋转的性质，等腰三角形的性质，熟练掌握旋转的性质是解题的关键．
练习册系列答案
相关题目
2．下面各整式能直接运用完全平方公式分解因式的是（ ）
| A． | x2-x+1 | B． | x2+2x-1 | C． | -2x+x2+1 | D． | 2x-x2+1 |
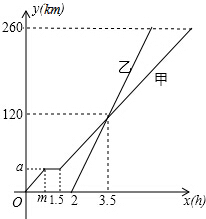甲、乙两车从A地匀速驶向B地，甲车比乙车早出发2小时，并且甲车图中休息了0.5小时后仍以原速度驶向B地，如图是甲、乙两车行驶的路程y（千米）与行驶的时间x（小时）之间的函数图象．下列说法：
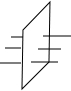如图，有红、黄、蓝粗细均匀的木棍各一根分别穿过木板，甲乙两人在木板的两侧同时随机抓住一根木棍，则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$．
17．下列二次根式中，不能与$\sqrt{3}$合并的是（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{12}$ | C． | $\sqrt{18}$ | D． | $\sqrt{27}$ |
14．
如图，将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF，若∠DAB=30°，则四边形CDFE的面积为（ ）
如图，将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF，若∠DAB=30°，则四边形CDFE的面积为（ ）| A． | 2cm2 | B． | 3cm2 | C． | 4cm2 | D． | 6cm2 |