题目内容
1.一个圆和等腰三角形ABC的两腰相切,切点是D,E,又和△ABC的外接圆相切于F.求证:△ABC的内心G和D,E在一条直线上.分析 设∠A=2α,AB=a,表示出AF=$\frac{a}{cosα}$,AK=acosα,KF=$\frac{asi{n}^{2}α}{cosα}$,再设OE=OF=b,表示出AO=$\frac{b}{sinα}$=AF-OF=$\frac{a}{cosα}$-b,再利用锐角三角函数表示即可.
解答 证明:如图,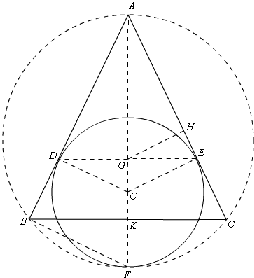
设∠A=2α,AB=a,由题意,△ABF,△AKB都是直角三角形.
∴AF=$\frac{a}{cosα}$,AK=acosα,KF=AF-AK=a($\frac{1}{cosα}$-cosα)=$\frac{asi{n}^{2}α}{cosα}$,
设OE=OF=b,
∴AO=$\frac{b}{sinα}$=AF-OF=$\frac{a}{cosα}$-b,
∴b(1+$\frac{1}{sinα}$)=$\frac{a}{cosα}$,
∴b=$\frac{asinα}{(sinα+1)cosα}$,
∴OG=bsinα=$\frac{asi{n}^{2}α}{(sinα+1)cosα}$,
∴AG=AO-GO=$\frac{acosα}{sinα+1}$,
过点G作AC的垂线,
∴GH=AGsinα=$\frac{asinαcosα}{sinα+1}$,
∴GK=OF-KF+OG=$\frac{asinα}{(sinα+1)cosα}$-$\frac{asi{n}^{2}α}{cosα}$+$\frac{asi{n}^{2}α}{(sinα+1)cosα}$=$\frac{asinαcosα}{sinα+1}$=GH,
∴G是三角形内心,
∴D,E,G三点共线.
点评 此题是三角形五心题,主要考查了锐角三角函数的意义,和判断三点共线的方法,解本题的关键是充分利用锐角三角函数的意义,难点是辅助线的作法.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案| A. | x≠3 | B. | x>$\frac{1}{2}$且x≠3 | C. | x≥2 | D. | x≥$\frac{1}{2}$且x≠3 |
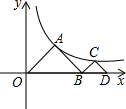 如图,△AOB,△CBD是等腰直角三角形,点A、C在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OB,BD都在x轴上,则点D的横坐标是4$\sqrt{2}$.
如图,△AOB,△CBD是等腰直角三角形,点A、C在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OB,BD都在x轴上,则点D的横坐标是4$\sqrt{2}$.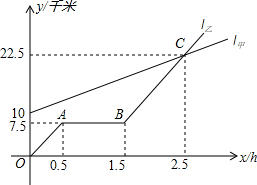 如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题:
如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题: 如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.
如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.