题目内容
如图，下列推理正确的有 ( )
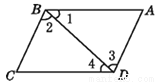
①∵∠1=∠4，∴BC//AD； ② ∵∠2=∠3，∴ AB//CD；
③ ∵∠BCD+∠ADC=180°，∴ AD//BC；
④ ∵∠1+∠2+∠A=180°，∴ BC//AD；
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①∵∠1=∠4，∴AB∥CD,故此选项错误；
② ∵∠2=∠3，∴AD∥BC,故此选项错误；
③ ∵∠BCD+∠ADC=180°，∴ AD//BC,故此选项正确；
④ ∵∠1+∠2+∠A=180°，∴ BC//AD,故此选项正确；
故选B.
一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表.
摸球 总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的次数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)10次试验“和为8”出现的频率是_________,20次试验“和为8”出现的频率是______,450次试验“和为8”出现的频率是__________;
(2)如果试验继续进行下去,根据上表数据,估计出现“和为8”的频率是_____________.
0.20 0.50 0.33 0.33
【解析】(1)10次试验“和为8”出现的频率是___0.20__,20次试验“和为8”出现的频率是_0.50_,450次试验“和为8”出现的频率是__0.33__;
(2) 利用图表得出：
实验次数越大越接近实际概率，所以出现“和为8”的概率是0.33． 我国作家莫言获得诺贝尔文学奖之后，他的代表作品《蛙》的销售量就比获奖之前增长了180倍，达到2100000册。把2100000用科学记数法表示为( )
A. 0.21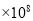
B. 2.1
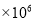C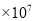. 2.1
D. 21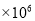
B
【解析】2100000=2.1×106. 如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
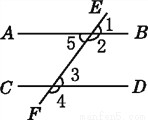
A. ∠1 B. ∠2 C. ∠4 D. ∠5
B
【解析】试题分析：A、∠3与∠1属于同位角，故本选项正确；B、∠3与∠2属于同旁内角，故本选项错误；
C、∠3与∠4于邻补角，故本选项错误；D、∠3与∠5于内错角，故本选项错误．
故选A． 已知：如图：∠1=∠2，∠3+∠4= 180°；确定直线a，c的位置关系，并说明理由；
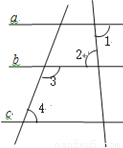
【解析】
a c；
理由：∵∠1=∠2（ ）,
∴ a // ( )；
∵ ∠3+∠4= 180°（ ）,
∴ c // ( )；
∵ a // ,c // ,
∴ // ( )；
答案见解析
【解析】试题分析：本题考查的是同学们对于平行线的判定的运用能力,内错角相等的两条直线平行；同旁内角互补的两条直线平行；平行于同一条直线的两条直线平行.
【解析】
a // c；
理由：∵∠1=∠2（ 已知 ）,
∴ a // b ( 内错角相等，两直线平行 )；
∵ ∠3+∠4= 180°（ 已知 ）,
∴ c // b ( 同旁内角互补， 两直线... 如图，下列说法正确的是 （ ）
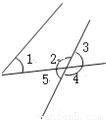
A. ∠1和∠2是内错角 B. ∠1和∠3是内错角
C. ∠1和∠4是内错角 D. ∠1和∠5是内错角
D
【解析】A. ∵∠1和∠2是同旁内角，故不正确；
B. ∵∠1和∠3是同位角，故不正确；
C. ∵ ∠1和∠4不具备特殊位置关系，故不正确；
D. ∵∠1和∠5是内错角，故正确；
故选D. 已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是70cm和48cm，则△ABC的腰和底边长分别为（ ）
A．24cm和22cm B．26cm和18cm
C．22cm和26cm D．23cm和24cm
C
【解析】
试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出△DBC的周长=AC+BC，再根据两个三角形的周长求出AB，然后BC的值即可．
【解析】
∵AB的垂直平分线交AC于D，
∴AD=BD，
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC，
∵△ABC和△DBC的周长分别是70cm和48cm，
∴... 已知：如图，AB=AD，BC=DE，AC=AE，BC交DE于点M、交AD于点N。求证：∠ 1 = ∠ 2 = ∠3。
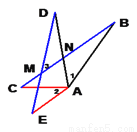
证明见解析
【解析】试题分析：由边边边证得△ABC≌△ADE，由全等三角形的性质得出∠BAC=∠DAE， ∠B=∠D，进而∠1=∠2，再由三角形内角和定理及等量代换即可得证.
在△ABC和△DCB中，
∴△ABC≌△ADE(SSS)，
∴∠BAC=∠DAE， ∠B=∠D，
即∠ 1+∠ DAC=∠ 2+∠ DAC，
∴∠1=∠2，
∵ ∠ 3+∠ DNM+... 一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF＝100°，那么∠BMD为( )
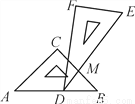
A. 95° B. 85° C. 90° D. 100°
B
【解析】∵∠ADF=100°，∠EDF=30°，
∴∠MDB=180°-∠ADF-∠EDF=180°-100°-30°=50°，
∴∠BMD=180°-∠B-∠MDB=180°-45°-50°=85°，
故选B.