题目内容
如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
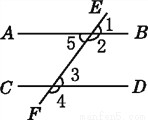
A. ∠1 B. ∠2 C. ∠4 D. ∠5
 B
【解析】试题分析:A、∠3与∠1属于同位角,故本选项正确;B、∠3与∠2属于同旁内角,故本选项错误;
C、∠3与∠4于邻补角,故本选项错误;D、∠3与∠5于内错角,故本选项错误.
故选A.
B
【解析】试题分析:A、∠3与∠1属于同位角,故本选项正确;B、∠3与∠2属于同旁内角,故本选项错误;
C、∠3与∠4于邻补角,故本选项错误;D、∠3与∠5于内错角,故本选项错误.
故选A.
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
计算:(每小题5分,共10分)
(1)5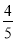 -2
-2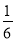 +(-4.8)+(-4
+(-4.8)+(-4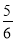 ) (2)-
) (2)-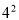 -3×
-3×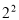 ×(
×(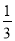 -1)÷(-1
-1)÷(-1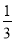 )
)
 (1)-6;(2)-22
【解析】试题分析:(1)利用加法的交换律和结合律计算,把一、三项结合,二、四项结合;(2)按照先算乘方,再算乘除,后算加减,有括号的先算括号里的顺序计算.
【解析】
(1)5-2+(-4.8)+(-4)
=5+(-4)+(-4)+(-2)
=1-7
=-6;
(2)--3××(-1)÷(-1)
=-16-3×4×(-) ×(-)...
(1)-6;(2)-22
【解析】试题分析:(1)利用加法的交换律和结合律计算,把一、三项结合,二、四项结合;(2)按照先算乘方,再算乘除,后算加减,有括号的先算括号里的顺序计算.
【解析】
(1)5-2+(-4.8)+(-4)
=5+(-4)+(-4)+(-2)
=1-7
=-6;
(2)--3××(-1)÷(-1)
=-16-3×4×(-) ×(-)... 如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
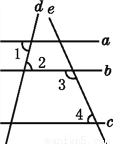
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
 已知;内错角相等,两直线平行;已知;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行
【解析】试题分析:根据平行线的性质得出a∥b,b∥c,即可推出答案.
试题解析:a∥c,
理由是:∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∵∠3+∠4=180°(已知),
∴b∥c(同旁内角互补,两直线平行),
∴a...
已知;内错角相等,两直线平行;已知;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行
【解析】试题分析:根据平行线的性质得出a∥b,b∥c,即可推出答案.
试题解析:a∥c,
理由是:∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∵∠3+∠4=180°(已知),
∴b∥c(同旁内角互补,两直线平行),
∴a... 如图,若∠1与∠2互补,∠2与∠4互补,则( )
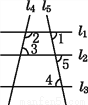
A. l4∥l5 B. l1∥l2 C. l1∥l3 D. l2∥l3
 C
【解析】∵∠1与∠2互补,∠2与∠4互补,
∴∠1=∠4(同角的补角相等),
∴l1∥l3 (内错角相等,两直线平行).
故选:C.
C
【解析】∵∠1与∠2互补,∠2与∠4互补,
∴∠1=∠4(同角的补角相等),
∴l1∥l3 (内错角相等,两直线平行).
故选:C. 如图,已知∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由;
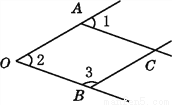
 AC//OB,OA//BC
【解析】试题分析:证明如下:如图所示,因为∠1=∠2,由“同位角相等,两直线平行”,可得AC//OB。又因为∠2=50°,∠3=130°,所以可得∠2=50°,∠3=130°,由“同旁内角互补,两直线平行”可得,OA//BC。
AC//OB,OA//BC;
理由: ∵∠1=50°,∠2=50° ( 已知 )
∴ ∠1=∠2
∴ AC//OB...
AC//OB,OA//BC
【解析】试题分析:证明如下:如图所示,因为∠1=∠2,由“同位角相等,两直线平行”,可得AC//OB。又因为∠2=50°,∠3=130°,所以可得∠2=50°,∠3=130°,由“同旁内角互补,两直线平行”可得,OA//BC。
AC//OB,OA//BC;
理由: ∵∠1=50°,∠2=50° ( 已知 )
∴ ∠1=∠2
∴ AC//OB... 如图,下列推理正确的有 ( )
①∵∠1=∠4,∴BC//AD; ② ∵∠2=∠3,∴ AB//CD;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD;
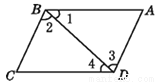
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】①∵∠1=∠4,∴AB∥CD,故此选项错误;
② ∵∠2=∠3,∴AD∥BC,故此选项错误;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC,故此选项正确;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD,故此选项正确;
故选B.
B
【解析】①∵∠1=∠4,∴AB∥CD,故此选项错误;
② ∵∠2=∠3,∴AD∥BC,故此选项错误;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC,故此选项正确;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD,故此选项正确;
故选B. 如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC交CA的延长线于点D,求∠ABD的度数.
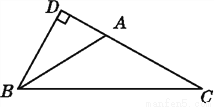
 30°.
【解析】试题分析:利用三角形的内角和为180°即可得到∠ABC或∠C的度数,进而利用外角可求得∠DAB的度数,从而求得∠ABD的度数.
试题解析:∵∠BAC=4∠ABC=4∠C,
∴∠BAC+∠ABC+∠C=180°,
即∠C=∠ABC=180×=30°,
∴∠DAB=∠C+∠ABC=30°+30°=60°,
∵BD⊥AC,
∴∠BDA=90°,...
30°.
【解析】试题分析:利用三角形的内角和为180°即可得到∠ABC或∠C的度数,进而利用外角可求得∠DAB的度数,从而求得∠ABD的度数.
试题解析:∵∠BAC=4∠ABC=4∠C,
∴∠BAC+∠ABC+∠C=180°,
即∠C=∠ABC=180×=30°,
∴∠DAB=∠C+∠ABC=30°+30°=60°,
∵BD⊥AC,
∴∠BDA=90°,... 如图,有6个条形方格图,图中由实线围成的图形中,全等图形有:①与___________;②与___________.
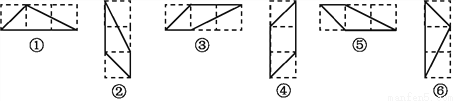
 ⑥ ③⑤
【解析】由全等图形的定义并观察图形可得①和⑥是全等图形,②、③和⑤是全等图形.
故答案为:⑥、③⑤
⑥ ③⑤
【解析】由全等图形的定义并观察图形可得①和⑥是全等图形,②、③和⑤是全等图形.
故答案为:⑥、③⑤ 
