题目内容
我国作家莫言获得诺贝尔文学奖之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到2100000册。把2100000用科学记数法表示为( )
A. 0.21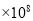 B. 2.1
B. 2.1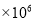 C. 2.1
C. 2.1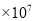 D. 21
D. 21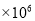
 B
【解析】2100000=2.1×106.
B
【解析】2100000=2.1×106.
练习册系列答案
相关题目
如图,关于虚线成轴对称的有( )个.

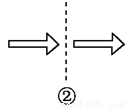
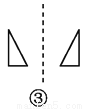
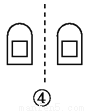
A. 1 B. 2 C. 3 D. 4
 B
【解析】①关于虚线不成轴对称,②关于虚线不成轴对称,③关于虚线不成轴对称,④关于虚线成轴对称,
故选B.
B
【解析】①关于虚线不成轴对称,②关于虚线不成轴对称,③关于虚线不成轴对称,④关于虚线成轴对称,
故选B. 计算:(每小题5分,共10分)
(1)5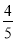 -2
-2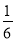 +(-4.8)+(-4
+(-4.8)+(-4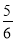 ) (2)-
) (2)-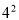 -3×
-3×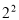 ×(
×(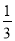 -1)÷(-1
-1)÷(-1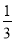 )
)
 (1)-6;(2)-22
【解析】试题分析:(1)利用加法的交换律和结合律计算,把一、三项结合,二、四项结合;(2)按照先算乘方,再算乘除,后算加减,有括号的先算括号里的顺序计算.
【解析】
(1)5-2+(-4.8)+(-4)
=5+(-4)+(-4)+(-2)
=1-7
=-6;
(2)--3××(-1)÷(-1)
=-16-3×4×(-) ×(-)...
(1)-6;(2)-22
【解析】试题分析:(1)利用加法的交换律和结合律计算,把一、三项结合,二、四项结合;(2)按照先算乘方,再算乘除,后算加减,有括号的先算括号里的顺序计算.
【解析】
(1)5-2+(-4.8)+(-4)
=5+(-4)+(-4)+(-2)
=1-7
=-6;
(2)--3××(-1)÷(-1)
=-16-3×4×(-) ×(-)... 如图是一个四棱柱和一个六棱锥,它们各有12条棱.
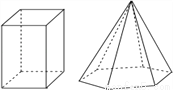
下列棱柱中和九棱锥的棱数相等的是( )
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱
 B
【解析】∵九棱锥有18条棱,五棱柱有15条棱, 六棱柱有18条棱,七棱柱有21条棱,八棱柱有24条棱,
∴六棱柱的棱数与九棱锥的棱数相等.
B
【解析】∵九棱锥有18条棱,五棱柱有15条棱, 六棱柱有18条棱,七棱柱有21条棱,八棱柱有24条棱,
∴六棱柱的棱数与九棱锥的棱数相等. 如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
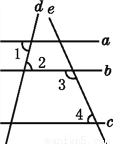
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
 已知;内错角相等,两直线平行;已知;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行
【解析】试题分析:根据平行线的性质得出a∥b,b∥c,即可推出答案.
试题解析:a∥c,
理由是:∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∵∠3+∠4=180°(已知),
∴b∥c(同旁内角互补,两直线平行),
∴a...
已知;内错角相等,两直线平行;已知;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行
【解析】试题分析:根据平行线的性质得出a∥b,b∥c,即可推出答案.
试题解析:a∥c,
理由是:∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∵∠3+∠4=180°(已知),
∴b∥c(同旁内角互补,两直线平行),
∴a... 如图,若∠1与∠2互补,∠2与∠4互补,则( )
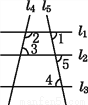
A. l4∥l5 B. l1∥l2 C. l1∥l3 D. l2∥l3
 C
【解析】∵∠1与∠2互补,∠2与∠4互补,
∴∠1=∠4(同角的补角相等),
∴l1∥l3 (内错角相等,两直线平行).
故选:C.
C
【解析】∵∠1与∠2互补,∠2与∠4互补,
∴∠1=∠4(同角的补角相等),
∴l1∥l3 (内错角相等,两直线平行).
故选:C. 如图,下列推理正确的有 ( )
①∵∠1=∠4,∴BC//AD; ② ∵∠2=∠3,∴ AB//CD;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD;
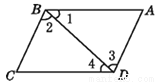
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】①∵∠1=∠4,∴AB∥CD,故此选项错误;
② ∵∠2=∠3,∴AD∥BC,故此选项错误;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC,故此选项正确;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD,故此选项正确;
故选B.
B
【解析】①∵∠1=∠4,∴AB∥CD,故此选项错误;
② ∵∠2=∠3,∴AD∥BC,故此选项错误;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC,故此选项正确;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD,故此选项正确;
故选B. 如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
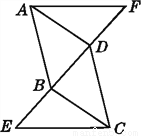
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
 (1)AD∥BC;(2)BF=DE
【解析】试题分析:(1)由“已知全等三角形的对应角相等”推知∠ADF=∠CBE,则等角的补角相等,即内错角∠ADB=∠CBD,则易证得AD∥BC;
(2)由“已知全等三角形的对应边相等”推知BE=DF,则根据等式的性质得到BE+BD=DF+BD,即BF=DE.
试题解析: (1)AD∥BC.理由如下:
∵△ADF≌△CBE,
∴∠A...
(1)AD∥BC;(2)BF=DE
【解析】试题分析:(1)由“已知全等三角形的对应角相等”推知∠ADF=∠CBE,则等角的补角相等,即内错角∠ADB=∠CBD,则易证得AD∥BC;
(2)由“已知全等三角形的对应边相等”推知BE=DF,则根据等式的性质得到BE+BD=DF+BD,即BF=DE.
试题解析: (1)AD∥BC.理由如下:
∵△ADF≌△CBE,
∴∠A... 

