题目内容
一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表.
摸球 总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的次数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)10次试验“和为8”出现的频率是_________,20次试验“和为8”出现的频率是______,450次试验“和为8”出现的频率是__________;
(2)如果试验继续进行下去,根据上表数据,估计出现“和为8”的频率是_____________.
 0.20 0.50 0.33 0.33
【解析】(1)10次试验“和为8”出现的频率是___0.20__,20次试验“和为8”出现的频率是_0.50_,450次试验“和为8”出现的频率是__0.33__;
(2) 利用图表得出:
实验次数越大越接近实际概率,所以出现“和为8”的概率是0.33.
0.20 0.50 0.33 0.33
【解析】(1)10次试验“和为8”出现的频率是___0.20__,20次试验“和为8”出现的频率是_0.50_,450次试验“和为8”出现的频率是__0.33__;
(2) 利用图表得出:
实验次数越大越接近实际概率,所以出现“和为8”的概率是0.33.
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
 (1) 红球约占40%,黄球约占60%;(2) 40个.
【解析】分析:(1)根据表格数据可以得到50次摸球实验活动中,出现红球20次,黄球30次,由此即可求出盒中红球、黄球各占总球数的百分比;(2)由题意可知50次摸球实验活动中,出现有记号的球4次,由此可以求出总球数,然后利用(1)的结论即可求出盒中红球.
本题解析: (1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,...
(1) 红球约占40%,黄球约占60%;(2) 40个.
【解析】分析:(1)根据表格数据可以得到50次摸球实验活动中,出现红球20次,黄球30次,由此即可求出盒中红球、黄球各占总球数的百分比;(2)由题意可知50次摸球实验活动中,出现有记号的球4次,由此可以求出总球数,然后利用(1)的结论即可求出盒中红球.
本题解析: (1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,... 如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.
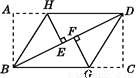
 见解析
【解析】试题分析:先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG.
试题解析:∵四边形ABCD是长方形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB...
见解析
【解析】试题分析:先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG.
试题解析:∵四边形ABCD是长方形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB... 如图,关于虚线成轴对称的有( )个.

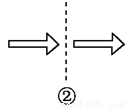
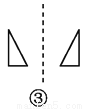
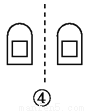
A. 1 B. 2 C. 3 D. 4
 B
【解析】①关于虚线不成轴对称,②关于虚线不成轴对称,③关于虚线不成轴对称,④关于虚线成轴对称,
故选B.
B
【解析】①关于虚线不成轴对称,②关于虚线不成轴对称,③关于虚线不成轴对称,④关于虚线成轴对称,
故选B. 计算:(每小题5分,共10分)
(1)5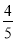 -2
-2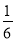 +(-4.8)+(-4
+(-4.8)+(-4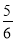 ) (2)-
) (2)-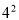 -3×
-3×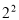 ×(
×(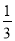 -1)÷(-1
-1)÷(-1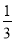 )
)
 (1)-6;(2)-22
【解析】试题分析:(1)利用加法的交换律和结合律计算,把一、三项结合,二、四项结合;(2)按照先算乘方,再算乘除,后算加减,有括号的先算括号里的顺序计算.
【解析】
(1)5-2+(-4.8)+(-4)
=5+(-4)+(-4)+(-2)
=1-7
=-6;
(2)--3××(-1)÷(-1)
=-16-3×4×(-) ×(-)...
(1)-6;(2)-22
【解析】试题分析:(1)利用加法的交换律和结合律计算,把一、三项结合,二、四项结合;(2)按照先算乘方,再算乘除,后算加减,有括号的先算括号里的顺序计算.
【解析】
(1)5-2+(-4.8)+(-4)
=5+(-4)+(-4)+(-2)
=1-7
=-6;
(2)--3××(-1)÷(-1)
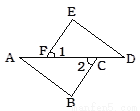
=-16-3×4×(-) ×(-)... 如图,下列推理正确的有 ( )
①∵∠1=∠4,∴BC//AD; ② ∵∠2=∠3,∴ AB//CD;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD;
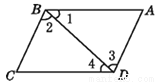
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】①∵∠1=∠4,∴AB∥CD,故此选项错误;
② ∵∠2=∠3,∴AD∥BC,故此选项错误;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC,故此选项正确;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD,故此选项正确;
故选B.
B
【解析】①∵∠1=∠4,∴AB∥CD,故此选项错误;
② ∵∠2=∠3,∴AD∥BC,故此选项错误;
③ ∵∠BCD+∠ADC=180°,∴ AD//BC,故此选项正确;
④ ∵∠1+∠2+∠A=180°,∴ BC//AD,故此选项正确;
故选B.