题目内容
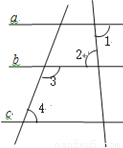
已知：如图：∠1=∠2，∠3+∠4= 180°；确定直线a，c的位置关系，并说明理由；
【解析】
a c；
理由：∵∠1=∠2（ ）,
∴ a // ( )；
∵ ∠3+∠4= 180°（ ）,
∴ c // ( )；
∵ a // ,c // ,
∴ // ( )；
答案见解析
【解析】试题分析：本题考查的是同学们对于平行线的判定的运用能力,内错角相等的两条直线平行；同旁内角互补的两条直线平行；平行于同一条直线的两条直线平行.
【解析】
a // c；
理由：∵∠1=∠2（ 已知 ）,
∴ a // b ( 内错角相等，两直线平行 )；
∵ ∠3+∠4= 180°（ 已知 ）,
∴ c // b ( 同旁内角互补， 两直线...
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
(1) 红球约占40%,黄球约占60%；(2) 40个.
【解析】分析：（1）根据表格数据可以得到50次摸球实验活动中，出现红球20次，黄球30次，由此即可求出盒中红球、黄球各占总球数的百分比；（2）由题意可知50次摸球实验活动中，出现有记号的球4次，由此可以求出总球数，然后利用（1）的结论即可求出盒中红球．
本题解析： (1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,... 如图是一个四棱柱和一个六棱锥，它们各有12条棱．
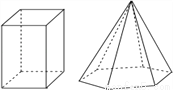
下列棱柱中和九棱锥的棱数相等的是（ ）
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱
B
【解析】∵九棱锥有18条棱，五棱柱有15条棱， 六棱柱有18条棱，七棱柱有21条棱，八棱柱有24条棱，
∴六棱柱的棱数与九棱锥的棱数相等. 如图,若∠1与∠2互补,∠2与∠4互补,则( )
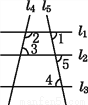
A. l4∥l5 B. l1∥l2 C. l1∥l3 D. l2∥l3
C
【解析】∵∠1与∠2互补，∠2与∠4互补，
∴∠1=∠4(同角的补角相等)，
∴l1∥l3 (内错角相等，两直线平行).
故选：C. 如图,∠1的内错角是( )
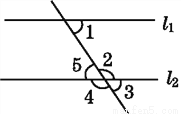
A. ∠2 B. ∠3 C. ∠4 D. ∠5
D
【解析】试题分析：根据内错角位于截线异侧，位于两条被截线之间可知∠1的内错角是∠5．
故选D． 如图，下列推理正确的有 ( )
①∵∠1=∠4，∴BC//AD； ② ∵∠2=∠3，∴ AB//CD；
③ ∵∠BCD+∠ADC=180°，∴ AD//BC；
④ ∵∠1+∠2+∠A=180°，∴ BC//AD；
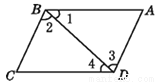
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①∵∠1=∠4，∴AB∥CD,故此选项错误；
② ∵∠2=∠3，∴AD∥BC,故此选项错误；
③ ∵∠BCD+∠ADC=180°，∴ AD//BC,故此选项正确；
④ ∵∠1+∠2+∠A=180°，∴ BC//AD,故此选项正确；
故选B. 如图，已知在△ABC中，∠C=90°，AB的垂直平分线MN交BC于点D.
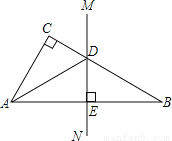
（1）如果∠CAD=20°，求∠B的度数；
（2）如果∠CAB=50°，求∠CAD的度数；
（3）如果∠CAD：∠DAB=1：2，求∠CAB的度数.
（1）∠B＝35°；（2）∠CAD=10°；（3）∠CAB=54°.
【解析】试题分析：（1）根据直角三角形的性质求出∠ADC=70°，根据线段的垂直平分线的性质得到DA=DB，计算即可；
（2）根据直角三角形的性质求出∠B的度数，根据线段的垂直平分线的性质得到DA=DB，计算即可；
（3）设∠CAD=x，根据题意列出方程，解方程即可．
试题解析：（1）∵∠C=90°，∠C... 如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否合乎要求,并说明理由.(电线杆的粗细忽略不计)
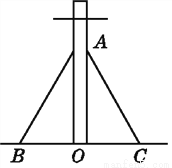
合乎要求.理由见解析.
【解析】试题分析：根据题意，证明△ABO≌△ACO即可得解.
试题解析:合乎要求.理由如下:
在△ABO和△ACO中,
所以△ABO≌△ACO(SAS).
所以∠BAO=∠CAO.所以合乎要求. 一角为80°的三角形中，另两角的角平分线相交所成的锐角是________．
50°
【解析】∵∠A=80°，
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°，
∵OB、OC分别是∠ABC、∠ACB的平分线，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=×100°=50°，
在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°-50°=130°，
∴∠CO...