题目内容
13.已知关于x的一元二次方程(x-3)(x-4)=|a|.(1)求证:对于任意实数a,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求a的值及方程的另一个根.
分析 (1)将原方程整理成一般式,再结合根的判别式即可得出△=4|a|+1>0,由此即可证出结论;
(2)将x=1代入一元二次方程中即可求出a值,设方程的另一个根为m,根据根与系数的关系即可得出1+m=7,解之即可得出方程的另一个根.
解答 (1)证明:原方程整理后可得:x2-7x+12-|a|=0,
∴△=(-7)2-4×(12-|a|)=4|a|+1>0,
∴对于任意实数a,方程总有两个不相等的实数根;
(2)解:将x=1代入x2-7x+12-|a|=0中,
1-7+12-|a|=0,解得:a=±6.
设方程的另一个根为m,
则有1+m=7,
解得:m=6.
∴a的值为±6,方程的另一个根为6.
点评 本题考查了根与系数的关系、一元二次方程的解以及根的判别式,解题的关键是:(1)熟练掌握“当△>0时,方程有两个不相等的实数根”;(2)将x=1代入原方程求出a值.

练习册系列答案
相关题目
18.计算a12÷a4(a≠0)的结果是( )
| A. | a3 | B. | a-8 | C. | a8 | D. | a-3 |
11.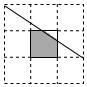 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{7}{8}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
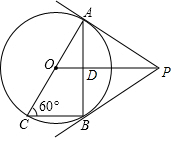 如图,已知AC是⊙O的直径,∠ACB=60°,连结AB,过A、B两点分别作⊙O的切线,两切线交于点P,连接OP交AB于D.
如图,已知AC是⊙O的直径,∠ACB=60°,连结AB,过A、B两点分别作⊙O的切线,两切线交于点P,连接OP交AB于D.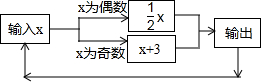 如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )
如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )